Question

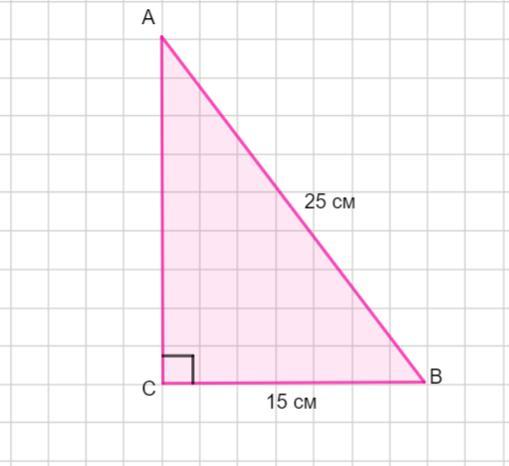
У трикутнику АВС кут С=90о , АВ=25см, ВС= 15см.Чому дорівнює синус кута В?

Answer 1

Ответ:

$sin B =0,8.$

Объяснение:

По условию задан ΔАВС - прямоугольный, так как ∠С=90°.

Гипотенуза АВ =25 см, катет ВС =15 см.

Надо определить синус угла В.

Воспользуемся теоремой Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

$AB^{2} =AC^{2} +BC^{2} ;\\AC^{2}=AB^{2} -BC^{2} ;\\AC= \sqrt{AB^{2} -BC^{2}} ;\\AC= \sqrt{25^{2} -15^{2} } =\sqrt{625-225} =\sqrt{400} =20$ см.

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе .

$sin B =\dfrac{AC}{AB} ;\\\\sin B =\dfrac{20}{25} =\dfrac{20:5}{25:5} =\dfrac{4}{5} =\dfrac{4\cdot2}{5\cdot2} =\dfrac{8}{10} =0,8$

#SPJ1