Предмет: Алгебра,
автор: Аноним
Помогите пожалуйста решить интеграл
Приложения:
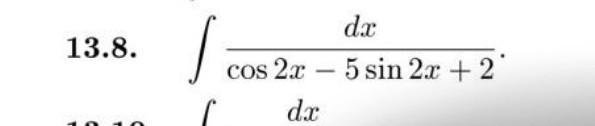
Ответы
Автор ответа:
1
Ответ:
Применяем универсальную тригонометрическую подстановку . В подынтегральной функции содержатся sin2x и cos2x, тогда тангенс половинного угла будет tgх .
Автор ответа:
0
Ответ:
решение написал и сфоткал зри
Объяснение:
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: эля633
Предмет: Английский язык,
автор: ПерсонэКарлеонэ
Предмет: Русский язык,
автор: chevelevava
Предмет: Другие предметы,
автор: dina449women
Предмет: Русский язык,
автор: vvlada20