определите, системой каких неравенств можно выразить множество точек, выделенных на чертеже.
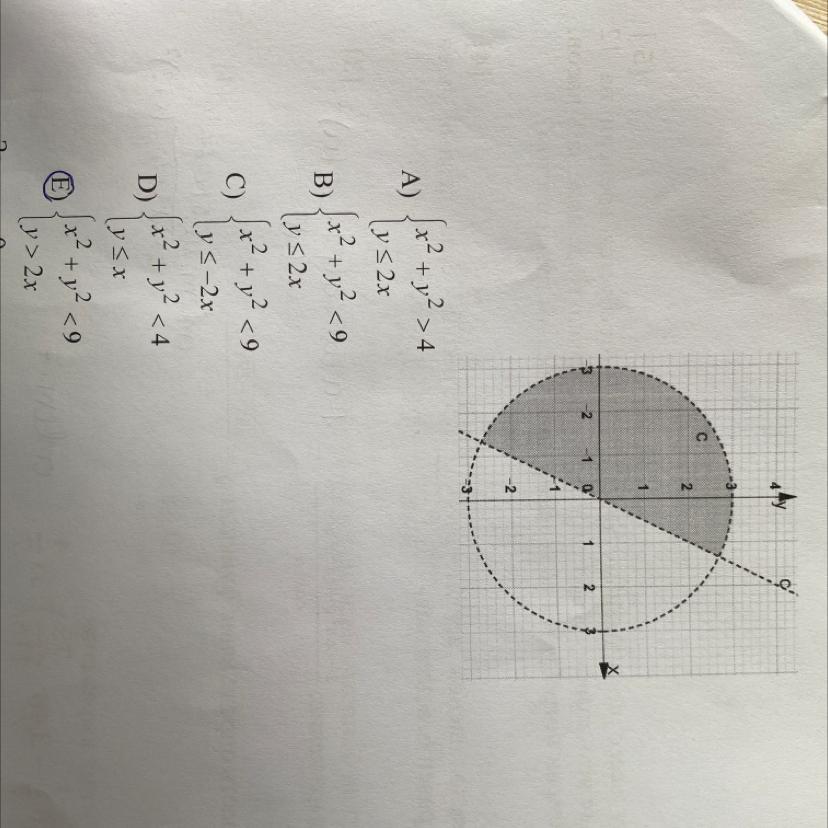
Ответы
Ответ:
система неравенств, выражающая множество точек выделенных на чертеже
Е)
Объяснение:
Прежде всего "упрячем" точки внутрь окружности.
Формула окружности
x² + y² = R²
По графику определяем радиус данной окружности.
R = 3
На графике окружность отмечена пунктирной линией. Это значит, что в искомое множество точек не входят точки, лежащие на самой окружности.
Т.е. неравенство у нас должно быть строгое.
Следовательно, множество точек ограничено неравенством
x² + y² < 9
Теперь перейдем к прямой.
Это прямая, проходящая через начало координат.
Следовательно, она имеет вид
у = кх.
Коэффициент к определяем из графика. Например, по точке (1; 2).
Коэффициент к = 2.
График функции
у = 2х
И нам нужны точки, лежащие выше графика функции у = 2х. Поскольку график изображен пунктирной линией, мы не включаем в искомое множество точек точки, лежащие на самой прямой. Т.е. мы снова имеем строгое неравенство.
Значит, искомое множество точек определяется неравенством
у > 2x
Вот мы и получили систему неравенств, выражающую множество точек выделенных на чертеже,
#SPJ1