Question

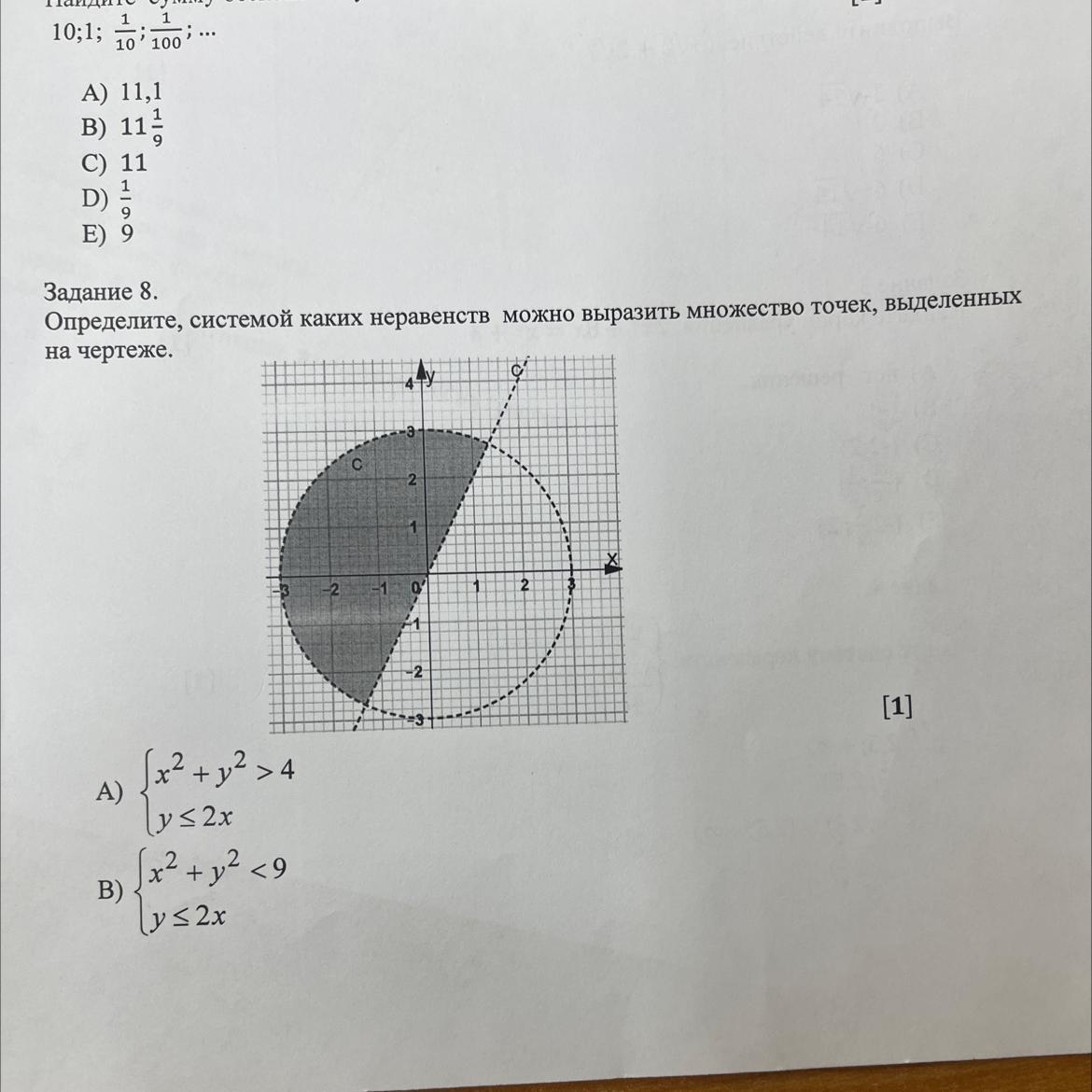
Определите, системой каких неравенств можно выразить множество точек, выделенных на чертеже. Пожалуйста

Answer 1

Ответ:

$\displaystyle \boldsymbol { \left \{ {{x^2+y^2 < 9} \atop {y > 2x\hfill}} \right. }$

Пошаговое объяснение:

Сначала ограничим множество точек кругом.

По графику определяем, что у нас окружность с центром в начале координат и радиусом 3

Уравнение такой окружности

x² + y² = 3²

Поскольку сама окружность отмечена на графике пунктиром, значит точки, расположенные на окружности не входят в искомое множество.

Таким образом, первое неравенство

x² + y²  < 9

Теперь переходим к прямой.

Она проходит через начало координат, значит имеет вид

y = kx

Коэффициент к найдем из координат любой точки.

Например (1; 2)  ⇒  2 = к*1  ⇒ k = 2

Итак, прямая у = 2х, отмечена пунктиром, нужна область, где значение у больше 2х.

Эта область огpаничивается неравенством

y > 2x

Тогда искомая система

$\displaystyle \left \{ {{x^2+y^2 < 9} \atop {y > 2x\hfill}} \right.$

#SPJ1