Предмет: Алгебра,
автор: SanchwerYT
Найдите область определения функции
Приложения:

Ответы
Автор ответа:
0
Ответ:
Область определения функции:
D(y) = (-∞; -3] ∪ [3; +∞).
Объяснение:
Найдите область определения функции:
- Подкоренное выражение неотрицательно.
То есть
3х² - 27 ≥ 0
Разложим на множители:
3(х² - 9) ≥ 0
3(х - 3)(х + 3) ≥ 0
Решим неравенство методом интервалов.
Приравняем левую часть к нулю и найдем корни:
3(х - 3)(х + 3) = 0
х = 3; х = -3.
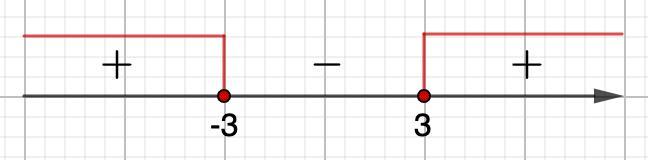
Отметим их на числовой оси и определим знаки выражения на промежутках.
См. рисунок.
Так как наше неравенство ≥ 0, то ответ будет на промежутках со знаком плюс:
х ∈ (-∞; -3] ∪ [3; +∞)
Область определения функции:
D(y) = (-∞; -3] ∪ [3; +∞).
#SPJ1
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: 20041004
Предмет: Русский язык,
автор: karimzhanova
Предмет: Қазақ тiлi,
автор: Жамал2006
Предмет: Математика,
автор: adema26
Предмет: Окружающий мир,
автор: zainvasgames