Question

З точки до кола проведено дві дотичних, кут між якими 60 градусів. Відстань від центра кола до даної точки 45 см. Знайдіть радіус кола.

Answer 1

Ответ:

Радіус кола дорівнює 22,5 см

Объяснение:

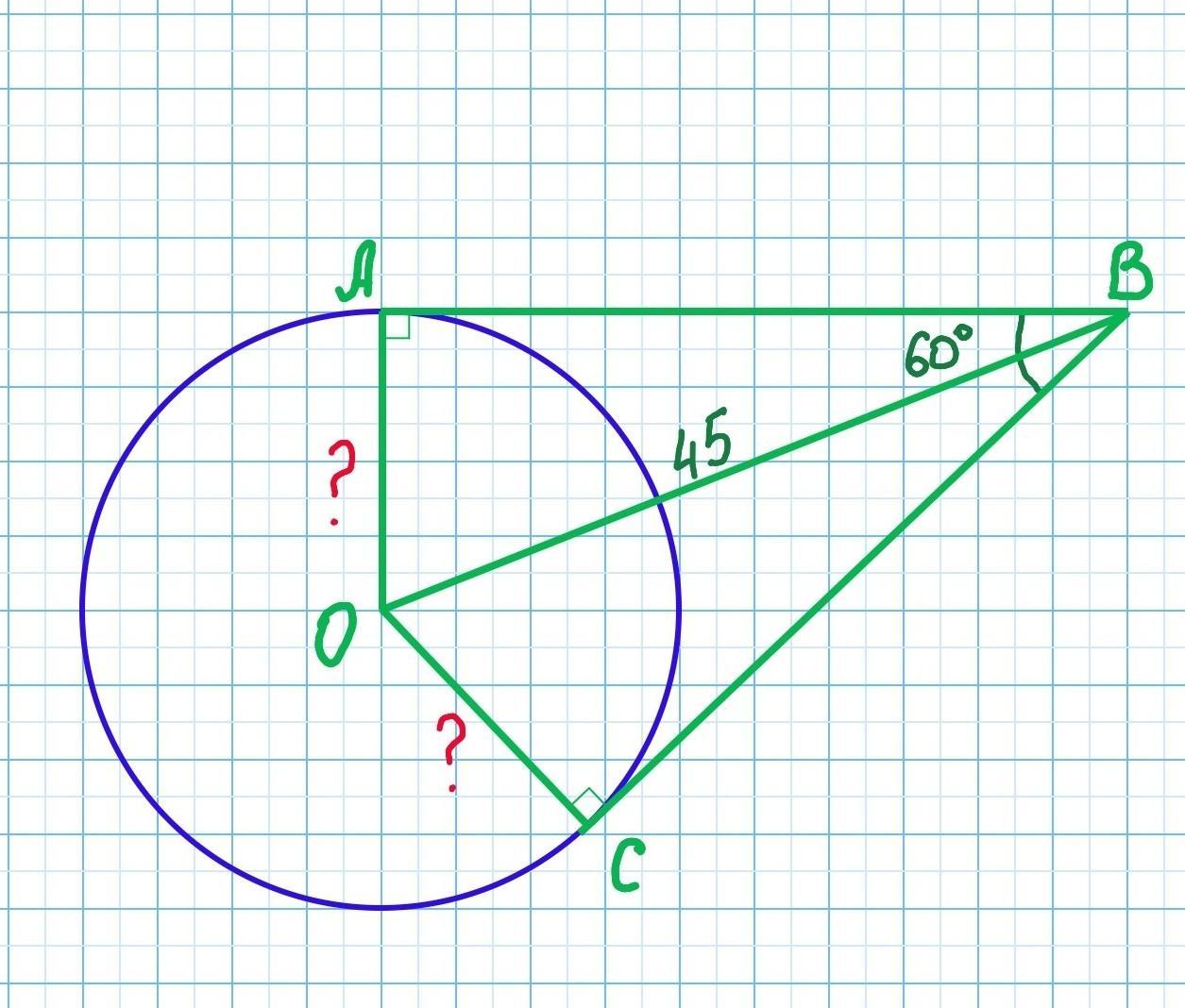
З точки В до кола проведено дві дотичних АВ І СВ, кут між ними: ∠АВС = 60°. Відстань від центра кола до даної точки ОВ = 45 см. Знайдемо радіус кола.

• Дотичною до кола називають пряму, яка має одну спільну точку з колом. Цю точку називають точкою дотику.
• Відстань від центра кола до точки дотику дорівнює радіусу кола.
• Дотична до кола перпендикулярна до радіуса, проведеного у точку дотику.
• Відрізки дотичних, проведених з однієї точки до кола рівні між собою.

Розв'язання

Так як АВ і СВ - дотичні до кола з центром в точці О, а ОА і ОС - радіуси кола, то АВ⟂ОА, СВ⟂ОС.

Розглянемо прямокутний трикутник АОВ і прямокутний трикутник СОВ.

ОВ - спільна, АВ=СВ, як відрізки дотичних, проведених з однієї точки.

△АОВ=△СОВ за гіпотенузою і катетом.

Якщо трикутники рівні, то елементи одного з них відповідно дорівнюють елементам другого: ∠АВО=∠СВО=∠АВС:2=60°:2=30°.

В прямокутному трикутнику катет, що лежить навпроти кута 30° дорівнює половині гіпотенузи:

ОА = R = ½•OB = ½•45 = 22,5 см.

#SPJ1