Предмет: Алгебра,
автор: buslaeffda
CРОЧНО 53 БАЛЛА!!!!!
Приложения:
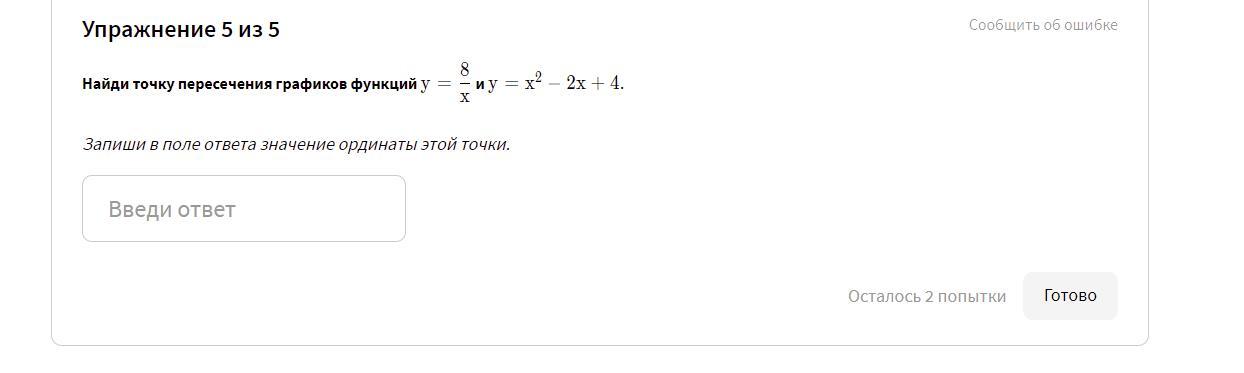
Ответы
Автор ответа:
1
Решение.
Найдём точки пересечения графиков функций, если приравняем "игреки" .
Ответ: точка пересечения графиков функций - это точка (2;4) .
Ордината точки пересечения у=4 .
Приложения:

buslaeffda:
а как я туда запишу это
у=4
см. скрин
Похожие вопросы
Предмет: Английский язык,
автор: nadejda04
Предмет: Русский язык,
автор: Kazuma24
Предмет: Қазақ тiлi,
автор: nutella123123
Предмет: Математика,
автор: elenakim57
Предмет: Химия,
автор: wkolnik2281337228228