геометрия
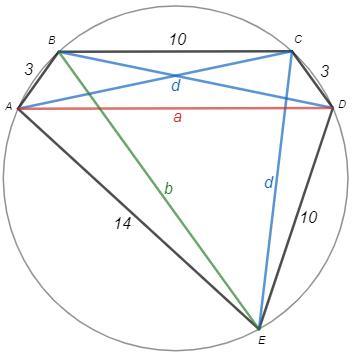
В выпуклом пятиугольнике ABCDE вписана окружность, где AB=CD=3, BC=DE=10 и АЕ=14. Сумма всех диагоналей пятиугольника ABCDE равна m/n, здесь m и n взаимно простые натуральные числа. Чему равно значение суммы m+n?
А 129
B 247
C 391
D 421
Ответы
Выпуклый пятиугольник ABCDE вписан в окружность, AB=CD=3, BC=DE=10, АЕ=14. Сумма всех диагоналей пятиугольника m/n (несократимая дробь). Найти m+n.
Равные хорды являются боковыми сторонами равнобедренной трапеции.
(AB=CD => ◡AB=◡CD => ∠ADB=∠CBD => BC||AD)
Имеем две р/б трапеции, ABCD и BCDE.
Диагонали р/б трапеции равны, AC=BD=CE=d
AD=a, BE=b
Запишем т Птолемея для вписанного четырехугольника
(AC*BD =AB*CD +BC*AD)
ABCD: d^2 =9 +10a
BCDE: d^2 =100 +3b
EABD: ab =14d +30
(d^2-9)/10 * (d^2-100)/3 = 14d +30
d^4 -9d^2 -100d^2 +900 = 420d +900
d^3 -109d -420 =0
Ищем корни среди делителей 420 = 3*4*5*7 или раскладываем на множители.
d^3 -144d +35d -12*35 =0
d(d^2-12^2) +35(d-12) =0
(d-12)(d^2 +12d +35) =0
Корень 12. Другие корни отрицательные (-5 и -7).
d=12
a=(144-9)/10 =27/2
b=(144-100)/3 =44/3
m/n = 3d +a +b =36 +27/2 +44/3 =385/6
m+n =391