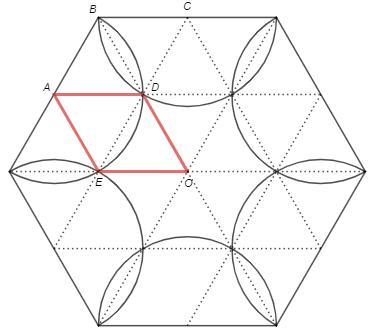
геометрия №11
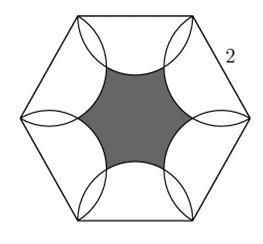
Как показано на рисунке, если 6 полуокружностей с диаметром 2 построены принимая сторону правильного шестиугольника как диаметр, найдите площадь закрашенной части.
варианты:
a) 6√3 - 3п
b) 9√3/2 - 2п
с) 3√3/2 - 2п
d) 3√3 - п
Ответы
Ответ:
Нам нужно найти площадь области заключенную двумя окружностями.
Так как диаметр окружности 2, то сторона тоже соответственно 2, а радиус окружности 1.
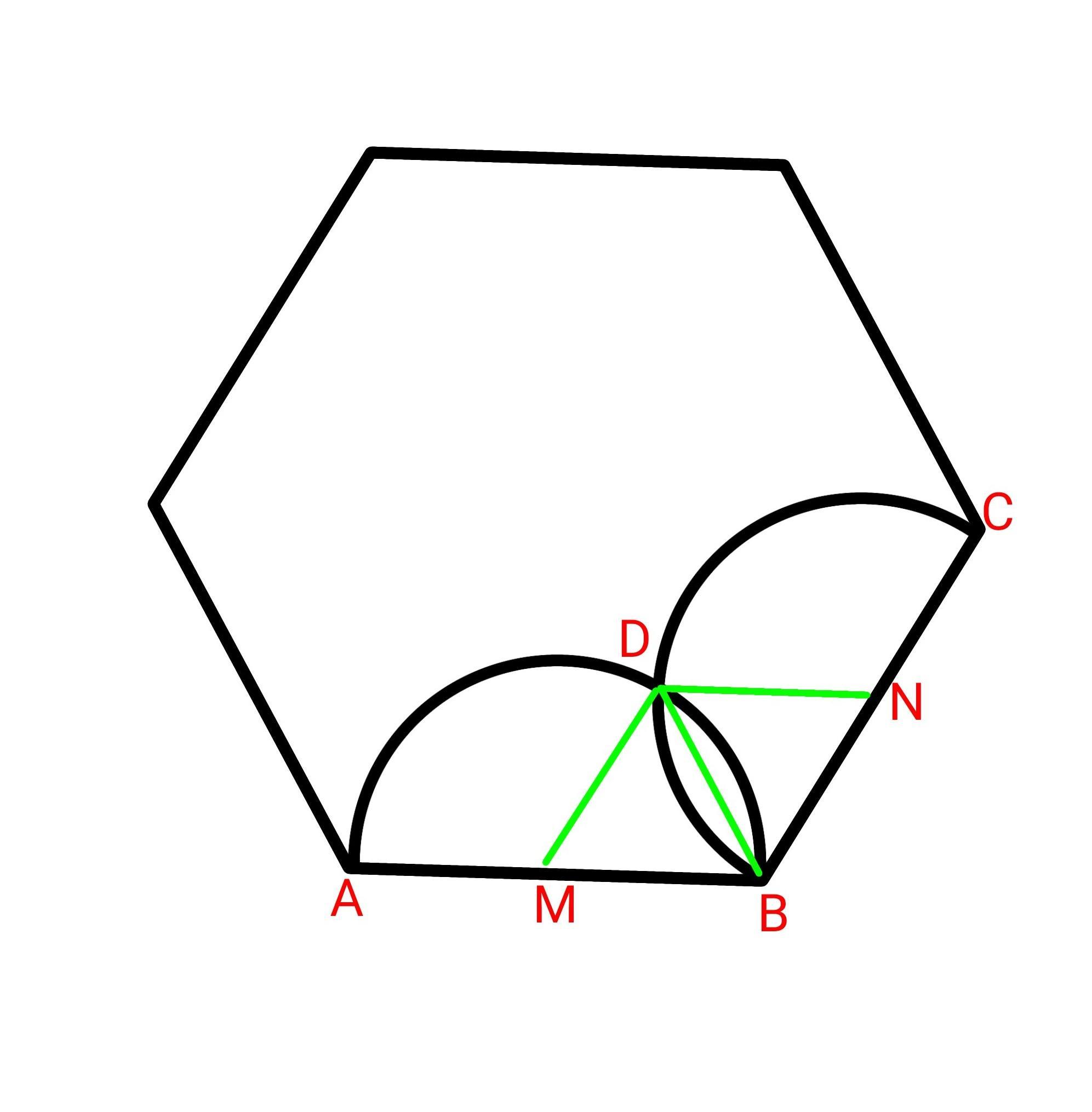
MB=NB=1
Если провести отрезок BD, то получается, что это биссектриса, потому что окружности равны и шестиугольник правильный.
ΔMBD и ΔBND равносторонние.
Найдем площадь меньшего сегмента круга с центром M заключенную хордой BD.
Площадь сегмента круга:
α в радианах
У нас треугольники правильные, поэтому α=60°=π/3
А полная площадь области между двумя окружностями будет
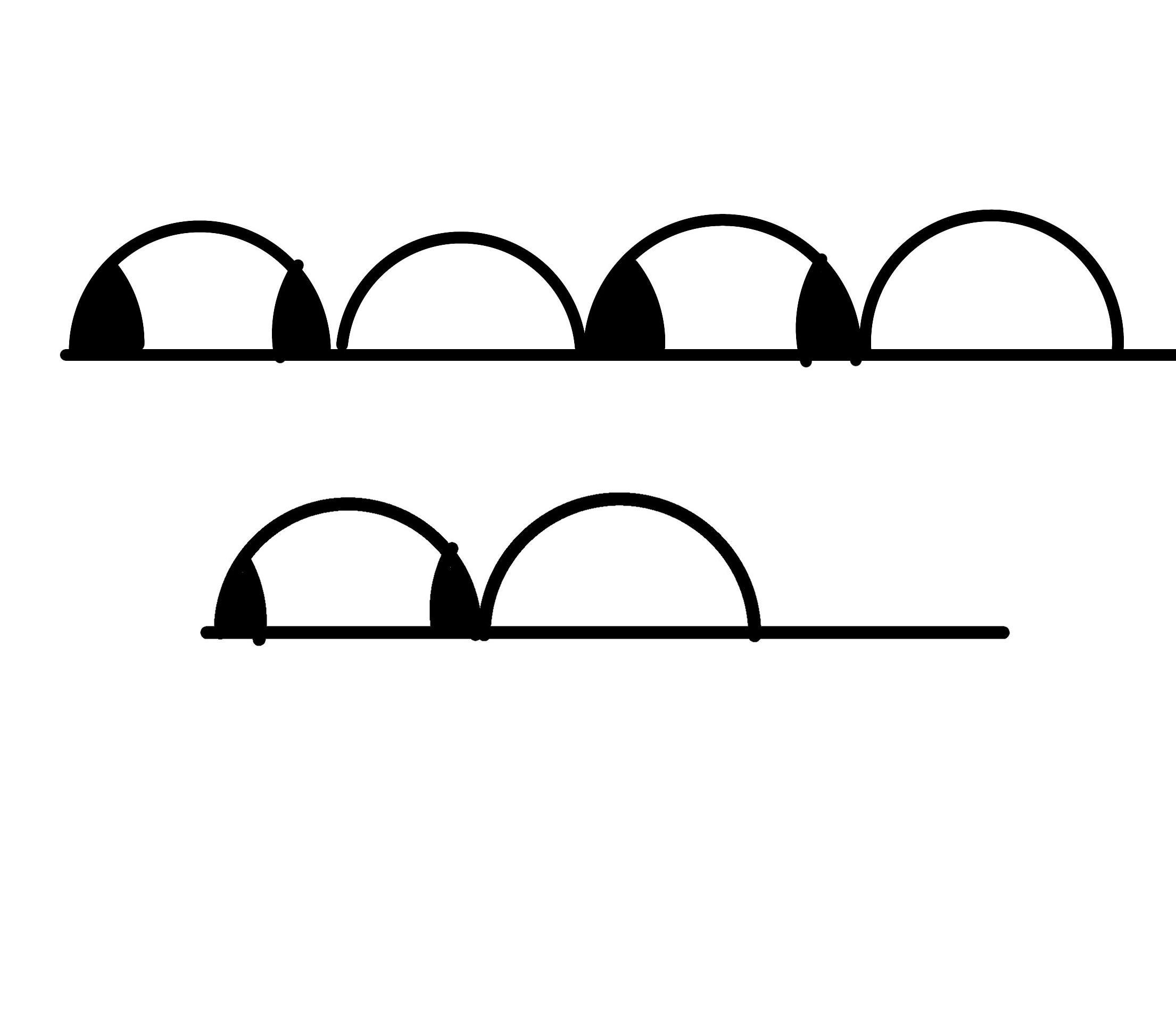
Теперь надо разделить эти полукруги и посчитать у скольких надо взять площадь, которую нашли выше, а у скольких не надо. У 3 нужно и у 3 не нужно, потому что у 2 кругов будет общая площадь.
Теперь посчитаем какова площадь всех 6 полукругов. Площадь круга πr², а нам нужна половина.
Но у нас их целых шесть, поэтому
А еще отнимем от этого результата 3 площади, заключенных между двумя кругами.
Это у нас получилась площадь кругов на фото.
Площадь всего шестиугольника:
Если что, сторона равна диаметру.
Теперь отнимем от всей площади шестиугольника площадь кругов.
Ответ: b)
Правильный шестиугольник можно разбить на правильные треугольники. Задача решается на сетке из равносторонних треугольников.
ABCD - ромб с углом 120°, угол BAD=60°
Понимаем, что точки D и Е находятся в узлах сетки.
Площадь ромба ADOE равна двум единичным треугольникам
= 2 * 1/2 *1 *√3/2 =√3/2
Площадь сектора ADE единичной окружности, угол 60°
= п 1^2 /6 =п/6
Вычитая из ромба сектор получим 1/6 искомой площади.
Ответ: 6(√3/2 -п/6) =3√3 -п