Предмет: Математика,
автор: versachexdior
матем задача №10
Вычислите:

sangers1959:
Помогу через 1 час.
хорошо)
ответ 0,5
значит 1/2 да?)))
варианты: 1, 1/2, 1/4, -1/2
1/2
благодарю
Ответы
Автор ответа:
3
Найти значение выражения (cos(2π/15) + cos (4π/15)) - (cos(7π/15)+cos(π/15)).
Ответ:
0,5 либо 1/2.
Формула:
Пошаговое объяснение:
Раскрываем скобки:
Поменяем порядок слагаемых/вычитаемых следующим образом:
Применяем вышеуказанную формулу разности косинусов в обеих скобках:
sin -a = - sin a; sin (π/6) = 1/2. Подставляем:
Переводим радианы в градусы:
вау! спасибо тебе большое)))
не за что)
Автор ответа:
1
Ответ:
0,5
Пошаговое объяснение:
во вложении
Приложения:
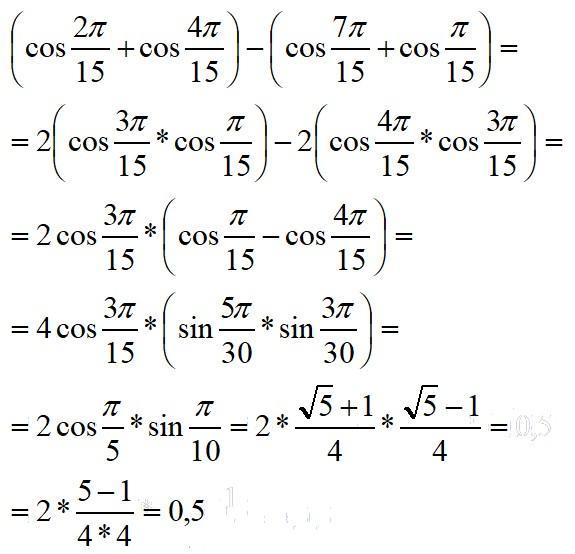

Похожие вопросы
Предмет: Английский язык,
автор: Zablotskiy
Предмет: Українська література,
автор: Настюша0901
Предмет: Українська мова,
автор: Vladik1dance1
Предмет: Химия,
автор: czibizovbogdan04
Предмет: Геометрия,
автор: PatHat