Предмет: Математика,
автор: versachexdior
матем задача №7 Сколько корней имеет уравнение: |x| (x²-4)= -1
IUV:
навскидку - 4 корня
спасибо)))
можно и без картинок : x = 0 - не является корнем и если x - корень , то и ( - x) - также корень , поэтому достачно доказать , что положительных корней ровно 2 , пусть x >0 и f(x) = x^3 -4x+1 ; f(-3) <0 ; f(-1) > 0 , значит есть отрицательный корень , f(0) >0 ; f(1) <0 и f(1) <0 ; f(2) > 0 , значит есть 2 положительных корня , а так как у f(x) корней не больше трёх , то значит положительных ровно 2
4 или 2?
каждому положительному соответствует противоположный ему по знаку , так как положительных ровно 2 , то всего корней 4
а поняла, спасибо)
функция в уравнении - чётная
a)4; b)3; c)2; d)∅
какой вариант выбрать?
ну конечно первый - 4 корня , просто картинки красивые , но нуждаются в дополнительном обосновании , например , почему минимумы ниже прямой y = -1 ? , но если вам нужен только ответ , то 4 корня
Ответы
Автор ответа:
1
4
На фото есть график,где видно )))
Приложения:
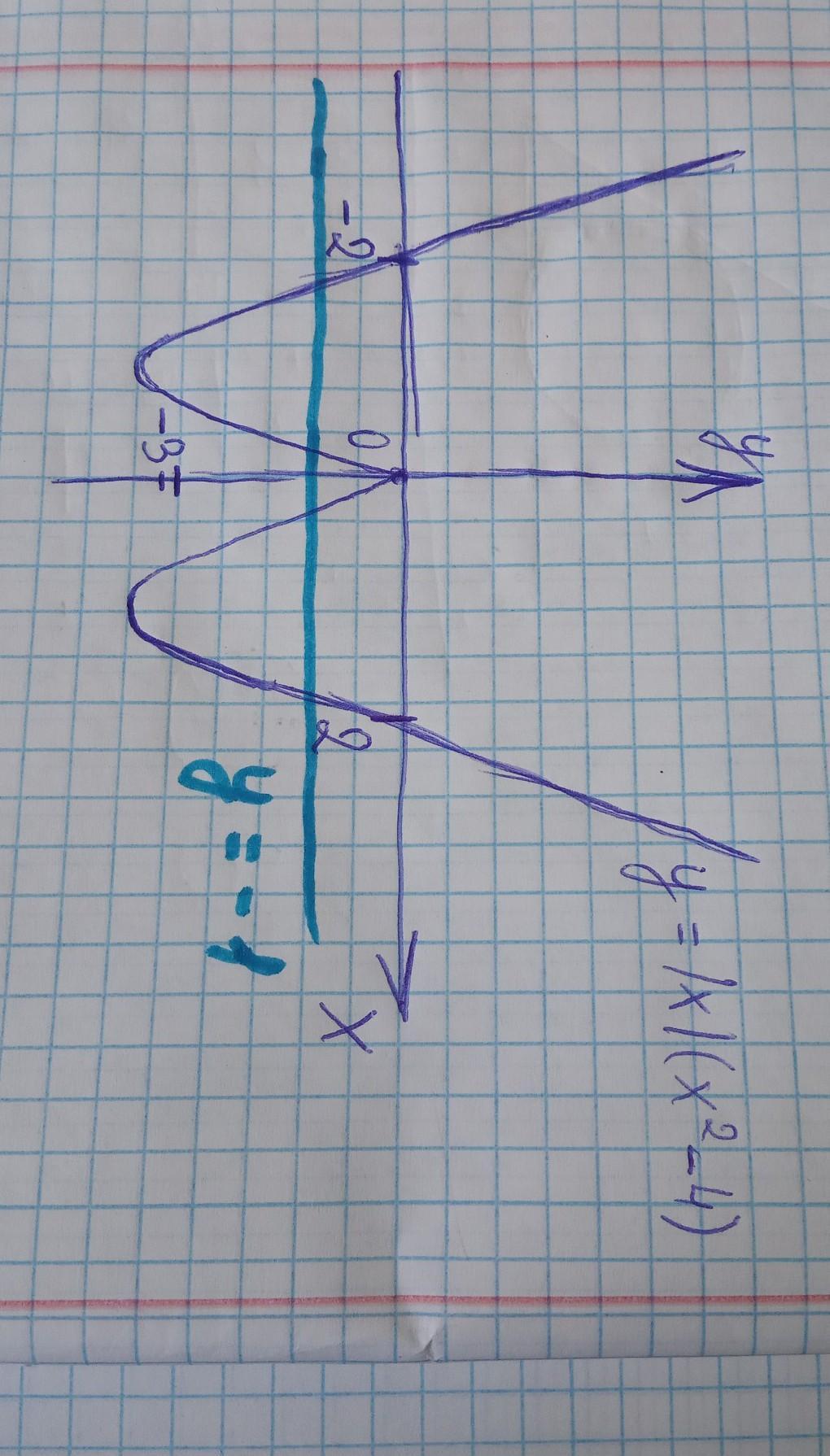
спасибо!!!
Автор ответа:
1
Ответ:
4 корня
Пошаговое объяснение:
графики во вложении
Приложения:
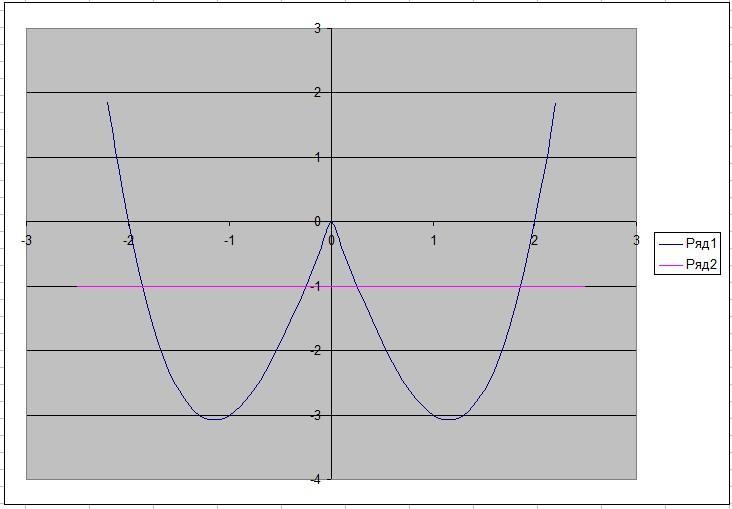
спасибо
на здоровье
Похожие вопросы
Предмет: Английский язык,
автор: yula231
Предмет: Українська мова,
автор: icanfly12
Предмет: Английский язык,
автор: Alisa2409
Предмет: Астрономия,
автор: 2denis9
Предмет: Русский язык,
автор: sasha163122