Предмет: Математика,
автор: OlegTretyakov
Найти область значения функции:
Распишите ваше решение по подробнее, пожалуйста.
Буду очень благодарен за помощь!
Приложения:
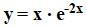
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
поскольку х∈R и >0, а при х=-∞ e^{-2x}=+∞, то
-∞
при х=+∞ у==∞/∞ =0 т.к. е^(2x) стремится к +∞ гораздо быстрее х (х и е^(2х) - функции возрастающие)
далее найдем точки экстремумов
y'=
y'=0 при x=0.5 ___+___0.5____-____ и в этой точке имеем максимум
≈0.18394
стало быть E(f)=(-∞;0.18394]
OlegTretyakov:
Спасибо за решение, а можете сказать, пожалуйста, откуда вы взяли x=0.5?
из решения уравнения 1-2х=0
понял теперь, спасибо еще раз, очень помогли
да, я там немного добавил
Похожие вопросы
Предмет: Русский язык,
автор: YULIAPETROVA84
Предмет: Русский язык,
автор: ejjejekekes
Предмет: Английский язык,
автор: Ксюша8910
Предмет: Химия,
автор: Аноним
Предмет: История,
автор: Аноним