Предмет: Геометрия,
автор: uachawa1681
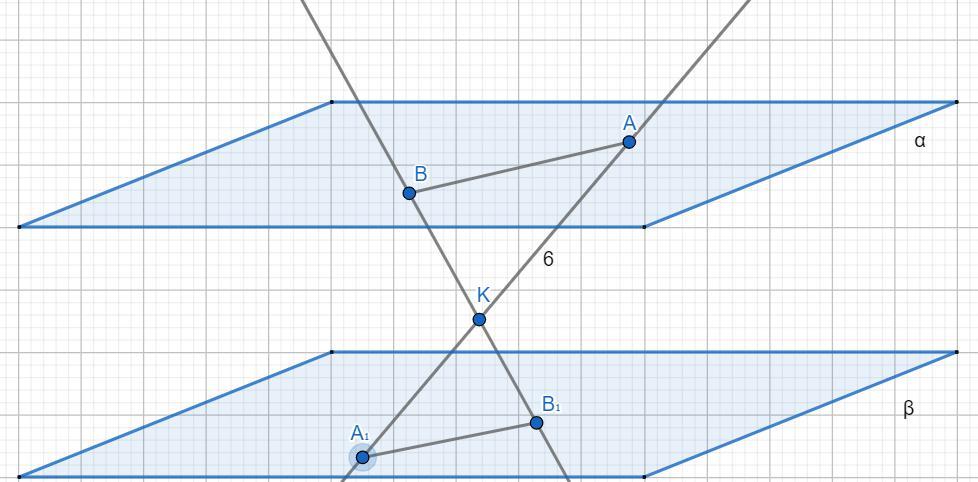
Плоскости α и β параллельны. Отрезок АВ расположен в плоскости α. Через его концы и точку К, лежащую между плоскостями, проведены прямые АК и ВК, пересекающие плоскость β в точках А1 и В1 соответственно. Найдите длину АА1, если АК=6дм, А1В1 : АВ = 3 : 4.
Ответы
Автор ответа:
0
Ответ:
Длина AA₁ = 105 см
Объяснение:
Линии пересечения двух параллельных плоскостей третьей плоскостью параллельны — значит параллельны отрезки AB и A₁B₁, лежащие в плоскости, образованной прямыми AA₁ и BB₁. Тогда треугольники ABK и A₁B₁K подобны по трем углам:
∠ABB₁ = ∠BB₁A₁ и ∠BAA₁ = ∠AA₁B₁ как накрест лежащие
∠AKB = ∠B₁KA₁ как вертикальные.
По условию А₁В₁ : АВ = 3 : 4 - тогда из подобия треугольников имеем, что и A₁K:AK = 3/4.
АК=6дм = 60 см - тогда A₁K =AK*3/4=60*3/4 = 90/2 см = 45 см
AA₁ = AK+KA₁ = 60+45=105 см
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: Masha22080601
Предмет: Русский язык,
автор: Дина2964
Предмет: Русский язык,
автор: veremiovamaria
Предмет: Биология,
автор: Blaaaaat