Question

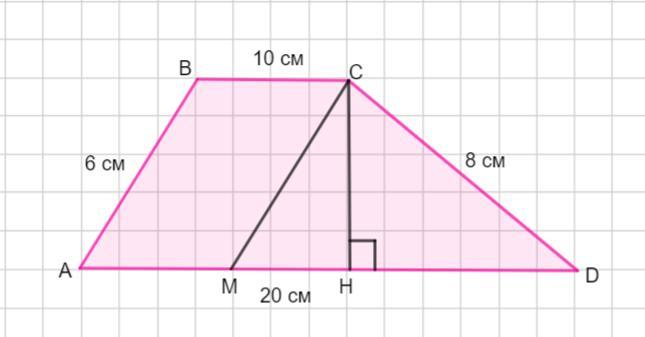
Знайти площу трапеції, якщо основи її дорівнюють 10см і 20см, а бічні сторони 6см і 8см.

Answer 1

Ответ:

Площадь трапеции равна 72 см ².

Объяснение:

Дана трапеция  ABCD . Основания ВС = 10 см , AD= 20 см , а боковые стороны АВ = 6 см, CD= 8 см.

Надо найти площадь трапеции. Площадь трапеции равна произведению полусуммы оснований на высоту трапеции.

Найдем высоту трапеции.

В трапеции ABCD  проведем СМ ║ АВ . Тогда АВСМ - параллелограмм , так как противолежащие стороны параллельны.

Тогда АВ = СМ = 6 см , ВС= АМ= 10 см и МD = 20 - 10 = 10 см.

Рассмотрим ΔМCD. По теореме , обратной теореме Пифагора ,

МD²=МС²+CD²

$10^{2} =6^{2} +8^{2} ;\\100=36+64;\\100=100$

ΔМCD - прямоугольный. Высота этого прямоугольного треугольника равна высоте трапеции.

Для того чтобы найти высоту прямоугольного треугольника, проведенную к гипотенузе, надо произведение катетов разделить на гипотенузу

$CH= \dfrac{CM\cdot CD}{MD } ;\\\\CH= \dfrac{6\cdot 8}{10 } =\dfrac{48}{10} =4,8;$

Тогда площадь трапеции будет равна

$S= \dfrac{BC+AD }{2} \cdot CH ;\\\\S= \dfrac{10+20 }{2} \cdot 4,8 =\dfrac{30}{2} \cdot 4,8= 15\cdot 4,8=72$

Значит, площадь трапеции равна 72 см ².

#SPJ1