Question

Помогите пожалуйста решить тест 1

Answer 1

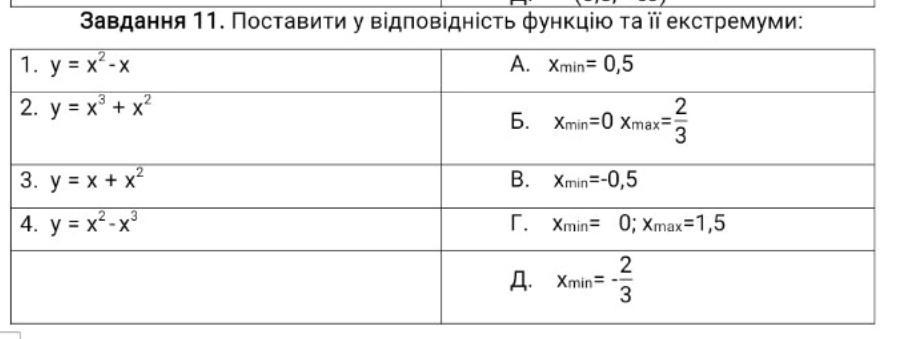
Установить соответствие между функциями и их точками эстремума:

1) y=x²-x; 2) у=х³+х²; 3) у=х+х²; 4) у=х²-х³.

Ответ:

1-А, 2-Г?, 3-В, 4-Б.

Объяснение:

Алгоритм нахождения точек эстремума функции:

1. Найти критические точки функции.
2. Исследовать характер изменения функции f(x) и знак производной f'(x) в промежутках, на которые найденные критические точки делят область определения функции y=f(x).
3. Относительно каждой критической точки определить, является ли она точкой максимума, минимума или не является точкой экстремума.

$\Large \boldsymbol {} 1)\ y=x^2-x\\\\x \in (-\infty; +\infty)\\\\y'=(x^2-x)'=2x^{2-1} -1=2x-1\\\\2x-1=0 \Leftrightarrow \boxed{x=0,5 \in[-2;1]}- \text{Krit. tochka}\\\\\\-----\boxed{0.5}+++++$

Переходя через точку х=0,5 производная функции меняет знак с минуса на плюс, соответственно х=0,5 - точка минимума функции.

$\Large \boldsymbol {}x_{min}=0.5$, 1-А.

$\Large \boldsymbol {}2)\ y=x^3+x^2\\\\x \in (-\infty; +\infty)\\\\y'=(x^3+x^2)'=3x^{3-1} +2x^{2-1} =3x^2+2x\\\\3x^2+2x=0 \\\\x(3x+2)=0 \\\\3x+2=0 \Leftrightarrow \boxed{x=-\frac{2}{3} \in[-2;1]}- \text{Krit. tochka}\\\\\boxed{x=0\in[-2;1]}- \text{Krit. tochka}\\\\\\++++\boxed{-\frac{2}{3} }----\boxed{0}++++$

Переходя через точку х=(-2/3) производная функции меняет знак с плюса на минус, соответственно х=(-2/3) - точка максимума функции.

Переходя через точку х=0 производная функции меняет знак с минуса на плюс, соответственно х=0 - точка минимума функции.

$\Large \boldsymbol {} x_{min}=0; x_{max}=-\frac{2}{3}$, 2-Г (только вместо 1,5 должно быть (-2/3), там ошибка).

$\Large \boldsymbol {} 3)\ y=x+x^2\\\\x \in (-\infty; +\infty)\\\\y'=(x+x^2)'=1+2x^{2-1} =1+2x\\\\1+2x=0 \Leftrightarrow \boxed{x=-0,5 \in[-2;1]}- \text{Krit. tochka}\\\\\\-----\boxed{-0.5}+++++$

Переходя через точку х=(-0,5) производная функции меняет знак с минуса на плюс, соответственно х=(-0,5) - точка минимума функции.

$\Large \boldsymbol {} x_{min}=0.5$, 3-В.

$\Large \boldsymbol {} 4)\ y=x^2-x^3\\\\x \in (-\infty; +\infty)\\\\y'=(x^2-x^3)'=2x^{2-1} -3x^{3-1} =2x-3x^2\\\\2x-3x^2=0 \\\\x(2-3x)=0 \\\\2-3x=0 \Leftrightarrow \boxed{x=\frac{2}{3} \in[-2;1]}- \text{Krit. tochka}\\\\\boxed{x=0\in[-2;1]}- \text{Krit. tochka}\\\\\\----\boxed{0}++++\boxed{\frac{2}{3} }----$

Переходя через точку х=2/3 производная функции меняет знак с плюса на минус, соответственно х=2/3 - точка максимума функции.

Переходя через точку х=0 производная функции меняет знак с минуса на плюс, соответственно х=0 - точка минимума функции.

$\Large \boldsymbol {} x_{min}=0; x_{max}=\frac{2}{3}$, 4-Б.