Предмет: Алгебра,
автор: vidchernigiv
знайдіть похідну функції, найдите походную функцию
Приложения:
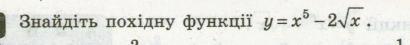
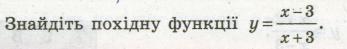
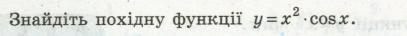
Ответы
Автор ответа:
2
Ответ:
1.
2.
3.
Объяснение:
Найти производную функций:
Используем формулы:
Найдем производную:
Производная частного:
Найдем производную:
Производная произведения:
Найдем производную:
#SPJ1
Похожие вопросы
Предмет: Русский язык,
автор: джон91
Предмет: Русский язык,
автор: noris74
Предмет: Русский язык,
автор: ETOya11
Предмет: История,
автор: arinabondarik2408
Предмет: Математика,
автор: kamilazarudneva