Question

Срочно даю 50баллов!!!

Answer 1

Ответ и Объяснение:

1. Решаем методом подстановки систему уравнений:

$\displaystyle \tt \left \{ {{x+y=5} \atop {3 \cdot x+y=7}} \right. \\\\\left \{ {{y=5-x} \atop {3 \cdot x+5-x=7}} \right. \\\\\left \{ {{y=5-x} \atop {2 \cdot x=2}} \right. \\\\\left \{ {{y=5-1=4} \atop {x=1}} \right.$

Ответ: (1; 5).

2. Решаем методом алгебраического сложения систему уравнений:

$\displaystyle \tt \left \{ {{4 \cdot x+3 \cdot y=2 } \atop {5 \cdot x+y=-3\;\;\; | \cdot (-3)}} \right. \\\\\left \{ {{4 \cdot x+3 \cdot y=2 } \atop {-15 \cdot x-3 \cdot y=9}} \right. \\\\\left \{ {{4 \cdot x+3 \cdot y=2 } \atop {-15 \cdot x-3 \cdot y+4 \cdot x+3 \cdot y=9+2}} \right. \\\\\left \{ {{4 \cdot x+3 \cdot y=2 } \atop {-11 \cdot x=11}} \right. \\\\\left \{ {{4 \cdot (-1)+3 \cdot y=2 } \atop {x=-1}} \right. \\\\\left \{ {{3 \cdot y=2+4 } \atop {x=-1}} \right.$

$\displaystyle \tt \left \{ {{3 \cdot y=6 } \atop {x=-1}} \right. \\\\\left \{ {{y=2 } \atop {x=-1}} \right.$

Ответ: (-1; 2).

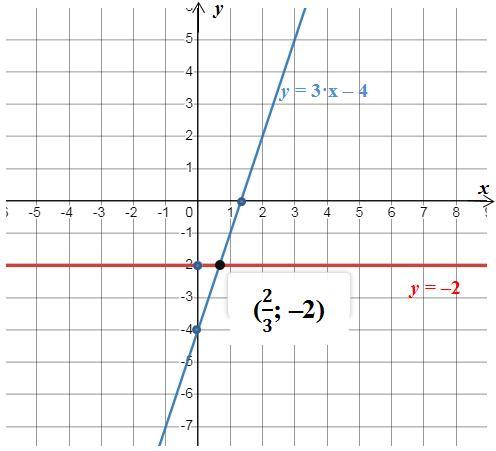
3. Решаем графическим методом систему уравнений:

$\displaystyle \tt \left \{ {{y=-2 } \atop {3 \cdot x-y=4}} \right.$

Преобразуем второе уравнение системы

$\displaystyle \tt \left \{ {{y=-2 } \atop {y=3 \cdot x-4}} \right.$

Обе функции системы прямые, причём первая функция параллельная прямая к оси Ох.

Для построения графика второй функции находим 2 точки, через которые проходит прямая:

y=0 ⇔ 3·x-4=0 ⇔ x = 4/3 = 1 1/3⇒ (1 1/3; 0);

x=0 ⇔ y(0) = 3·0 - 4 = -4 ⇒ (0; -4).

График в приложенном рисунке.

Как видим, функции пересекаются в точке (2/3; -2).

Ответ: (2/3; -2).

4. Решаем систему уравнений:

$\displaystyle \tt \left \{ {{6 \cdot (x-3)=7 \cdot y-1} \atop {2 \cdot (y+6)=3 \cdot x+2}} \right. \\\\\left \{ {{6 \cdot x-18=7 \cdot y-1} \atop {2 \cdot y+12=3 \cdot x+2}} \right. \\\\\left \{ {{6 \cdot x=7 \cdot y+17} \atop {2 \cdot y=3 \cdot x-10}} \right. \\\\\left \{ {{6 \cdot x=7 \cdot (1,5 \cdot x-5)+17} \atop {y=1,5 \cdot x-5}} \right. \\\\\left \{ {{6 \cdot x=10,5 \cdot x-35+17} \atop {y=1,5 \cdot x-5}} \right. \\\\\left \{ {{4,5 \cdot x=18} \atop {y=1,5 \cdot x-5}} \right.$

$\displaystyle \tt \left \{ {{x=18:4,5=4} \atop {y=1,5 \cdot 4-5=6-5=1}} \right.$

Ответ: (4; 1).

#SPJ1