Предмет: Алгебра,
автор: nurmuhameb123
Решите уравнение 3x-√x-2-16=0
Ответы
Автор ответа:
0
Ответ:
корень уравнения х = 6
Объяснение:
Определимся с ОДЗ.
х -2 ≥ 0; ⇒ х ≥ 2
3х - 16 ≥ 0; 3х ≥ 16; ⇒ х ≥ 16/3
Объединим два условия и получим х ≥ 16/3
Теперь решаем уравнение.
Возведем в квадрат обе части
9x² - 96x +256 = x - 2
9x² -97x + 258 = 0
D = b² - 4ac = (-97)² - 9288 = 121
Теперь посмотрим, входят ли корни в нашу ОДЗ
- этот корень подходит
- этот корень не подходит
Следовательно, корень уравнения х = 6
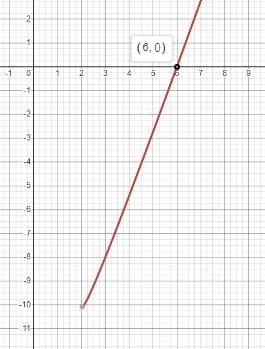
Для проверки привожу график функции
#SPJ1
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: Аноним
Предмет: Другие предметы,
автор: kare123
Предмет: Русский язык,
автор: гев8
Предмет: Математика,
автор: polinapasechnik2007
Предмет: Окружающий мир,
автор: Аноним