Предмет: Алгебра,
автор: arina271997
Вычислить определенный интеграл:
Приложения:
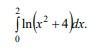
Ответы
Автор ответа:
2
Ответ:
Интегрирование по частям в определённом интеграле.
arina271997:
Спасибо
будь ласка , мені допоможіть , дуже потрібно ,завдання на теорію ймовірностей про нерівність Чебишова
NNNLLL54 можете помочь с алгеброй вопрос в профиле
Похожие вопросы
Предмет: Қазақ тiлi,
автор: denissavinov20
Предмет: Русский язык,
автор: davydovavaleri
Предмет: Английский язык,
автор: rusia34
Предмет: Математика,
автор: NRL
Предмет: Математика,
автор: jistdoit44