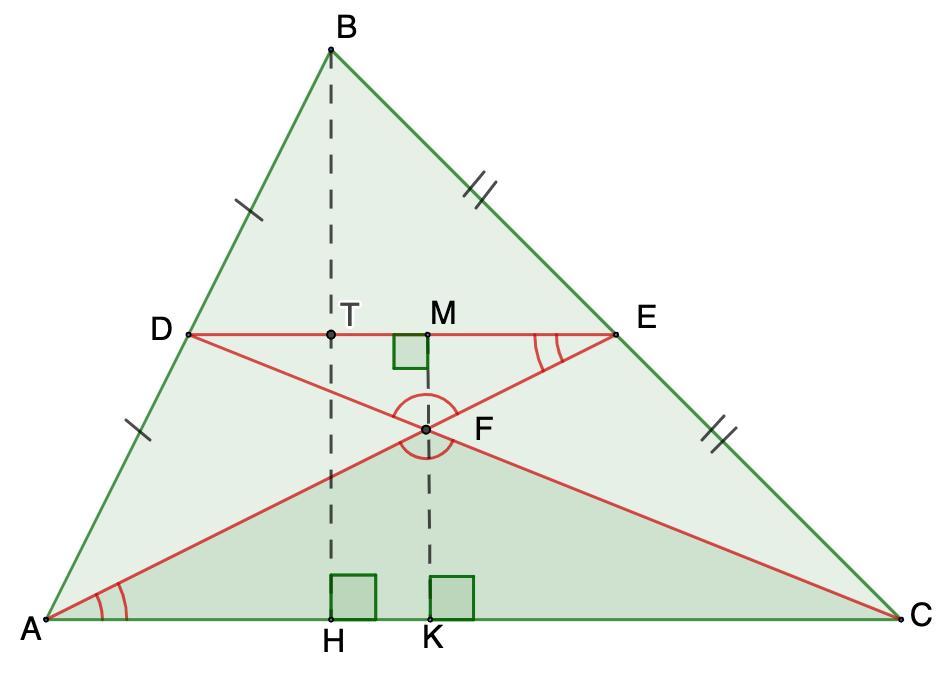
Предмет: Геометрия, автор: Lutiponchik

На малюнку зображено трикутник
ABC, DE – його середня лінія, а
F – точка
перетину діагоналей чотирикутника ADEC .
Знайдіть площу трикутника ABC
(у см² ), якщо
площа трикутника AFC
дорівнює 2см²

Ответы

Автор ответа: natalyabryukhova

Ответ:

Площадь треугольника АВС равна 6 см².

Объяснение:

Дан треугольник ABC, DE – его средняя линия, а F-точка пересечения диагоналей четырехугольника ADEC .

Найдите площадь треугольника ABC (в см²), если площадь треугольника AFC равен 2 см².

Дано: ΔАВС;

DE - средняя линия;

АЕ ∩ DC = F - диагонали ADEC;

S (AFC) = 2 см².

Найти: S (ABC).

Решение:

Проведем высоту ВН и высоту FК.

FК ∩ DE = М.

1. Рассмотрим ΔАВС.

DE - средняя линия (условие);

Средняя линия равна половине длины стороны, которую она не пересекает, и параллельна ей.

⇒ DE || AC; DE = $\displaystyle \frac{1}{2}$ AC.

2. Рассмотрим ΔFDE и ΔAFC.

⇒ ∠DFE = ∠AFC (вертикальные)

При пересечении двух параллельных прямых третьей, накрест лежащие углы равны.

⇒ ∠DЕF = ∠FАC (накрест лежащие при DE || AC и секущей АЕ)

ΔFDE ~ ΔAFC (по двум углам)

DE : AC = 1 : 2 (п.1)

⇒ FM : FK = 1 : 2

3. Пусть FM = h см, тогда FK = 2h см, а МК = 3h см.

S (AFC) = 2 см²

Площадь треугольника равна половине произведения стороны на высоту, проведенную к этой стороне.

$\displaystyle S(AFC) = \frac{1}{2}AC\cdot{FK}\\ \\2=\frac{1}{2}AC\cdot{2h}\\\\AC=\frac{2}{h}\;_{(CM)}$

4. Рассмотрим НТМК - прямоугольник.

⇒ НТ = МК = 3h см.

5. Рассмотрим ∠АВН.

DT || AH;

BD = DA (DE - средняя линия).

Если на одной из двух прямых отложить последовательно несколько равных между собой отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки. (т. Фалеса)

⇒ ВТ = ТН = 3h см, тогда ВН = 6h см.

6. Найдем площадь ΔАВС.

$\displaystyle S(ABC)=\frac{1}{2}AC\cdot{BH}=\frac{1}{2}\cdot{\frac{2}{h}\cdot6h }=6\;_{(CM^2)}$