Допоможіть хоть з якимось завданням будь ласка
Ответы
6) Если плоскость проходит через перпендикуляр к другой плоскости, то такие плоскости перпендикулярны.
SAB⊥ABC, т.к. SAB проходит через перпендикуляр AS к ABC.
7) Точка S равноудалена от сторон правильного треугольника и удалена от плоскости треугольника на расстояние √3 см. Найдите сторону треугольника, если точка S удалена от его сторон на 2√3 см.
Расстояние измеряется длиной перпендикуляра. Проведем перпендикуляры SK=SL=SM=2√3 к сторонам треугольника. Опустим перпендикуляр SO=√3 на плоскость треугольника.
△SOK=△SOL=△SOM по катету и гипотенузе
OK=OL=OM=3 (т Пифагора)
По т о трех перпендикулярах OK, OL, OM перпендикулярны сторонам треугольника и являются радиусами вписанной окружности. Сторона правильного треугольника =2√3 r =6√3 (см)
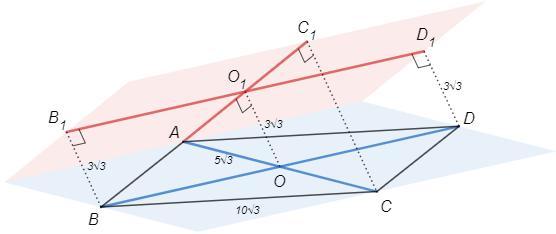
8) В ромбе со стороной 10√3 см и углом 120° через вершину тупого угла проведена плоскость на расстоянии 3√3 см от всех точек его большей диагонали. Найдите проекции диагоналей на эту плоскость.
В ромбе все стороны равны. Диагонали являются биссектрисами, перпендикулярны, точкой пересечения делятся пополам.
∠BAC=60° => △ABC - равносторонний.
AC=10√3
BO=AC√3/2 =15 (высота в △ABC)
BD=2BO =30
Чтобы получить проекцию отрезка, нужно опустить перпендикуляры из концов отрезка на плоскость.
Опустим перпендикуляры BB1 и DD1.
BB1=DD1 => BB1D1D - прямоугольник => B1D1=BD =30 (см)
Опустим перпендикуляры OO1 и СС1.
OO1=3√3
AO=AC/2 =5√3
AO1=4√3 (△OAO1, т Пифагора).
AO=OC => AO1=O1C1 (т Фалеса)
AC1=2AO1 =8√3 (см)