Предмет: Математика,
автор: bpu76924
СРОЧНО ПОМОГИТЕ!!!! ДАЮ 40 БАЛЛОВ!
Приложения:
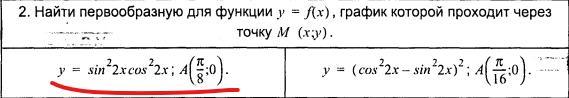
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Дана функция y = sin²2x·cos²2x и точка A(π/8; 0).
Требуется найти первообразную F(x) для заданной функции, проходящую через точку А, то есть такую первообразную, для которой F(π/8) = 0.
Решение. Находим первообразную F(x) для заданной функции:
Теперь определим первообразную, которая проходит через точку А:
Искомая первообразная
#SPJ1
Похожие вопросы
Предмет: Қазақ тiлi,
автор: usovakaty2003
Предмет: Русский язык,
автор: kloitghjk
Предмет: Русский язык,
автор: danil516
Предмет: История,
автор: kozitsinana