Question

1. Постройте график функции $y=\frac{2-x}{x^{2}+x-6}$
2.Определите область значений этой функции

Answer 1

$y=\dfrac{2-x}{x^2+x-6}$

В самом начале нужно найти область определения функции. Для этого предварительно разложим знаменатель на множители:

$x^2+x-6=x^2+3x-2x-6=x(x+3)-2(x+3)=(x+3)(x-2)$

То же самое можно было сделать, найдя корни квадратного трехчлена:

$x^2+x-6=0$

$D=1^2-4\cdot1\cdot(-6)=1+24=25$

$x_1=\dfrac{-1-\sqrt{25} }{2\cdot 1} =-3$

$x_2=\dfrac{-1+\sqrt{25} }{2\cdot 1} =2$

$\Rightarrow x^2+x-6=(x-(-3))(x-2)=(x+3)(x-2)$

Так или иначе, функция приняла вид:

$y=\dfrac{2-x}{(x+3)(x-2)}$

Находим область определения. Дробь определена, когда знаменатель не равен нулю:

$(x+3)(x-2)\neq 0$

$\Rightarrow x\neq -3;\ x\neq 2$

Таким образом, область определения функции:

$D(y)=(-\infty;\ -3)\cup(-3;\ 2)\cup(2;\ +\infty)$

Перед построением графика, упростим выражение функции. Воспользуемся одним из свойств дроби и поменяем знаки перед дробью и в числителе дроби. Получим:

$y=\dfrac{2-x}{(x+3)(x-2)}=-\dfrac{-(2-x)}{(x+3)(x-2)}=-\dfrac{x-2}{(x+3)(x-2)}$

Можем сократить:

$y=-\dfrac{x-2}{(x+3)(x-2)}=-\dfrac{1}{x+3}$

Строим график функции. График функции $y=-\dfrac{1}{x+3}$ получается из графика функции $y=-\dfrac{1}{x}$ путем его переноса на 3 единицы влево вдоль оси x. В свою очередь, график функции $y=-\dfrac{1}{x}$ представляем собой график функции $y=\dfrac{1}{x}$, отраженный относительно оси x.

Функция $y=\dfrac{1}{x}$ - типовая гипербола, для построения можно использовать несколько точек:

$x=\pm1\Rightarrow y=\dfrac{1}{\pm1} =\pm1$

$x=\pm2\Rightarrow y=\dfrac{1}{\pm2} =\pm0.5$

$x=\pm0.5\Rightarrow y=\dfrac{1}{\pm0.5} =\pm2$

$x=\pm4\Rightarrow y=\dfrac{1}{\pm4} =\pm0.25$

$x=\pm0.25\Rightarrow y=\dfrac{1}{\pm0.25} =\pm4$

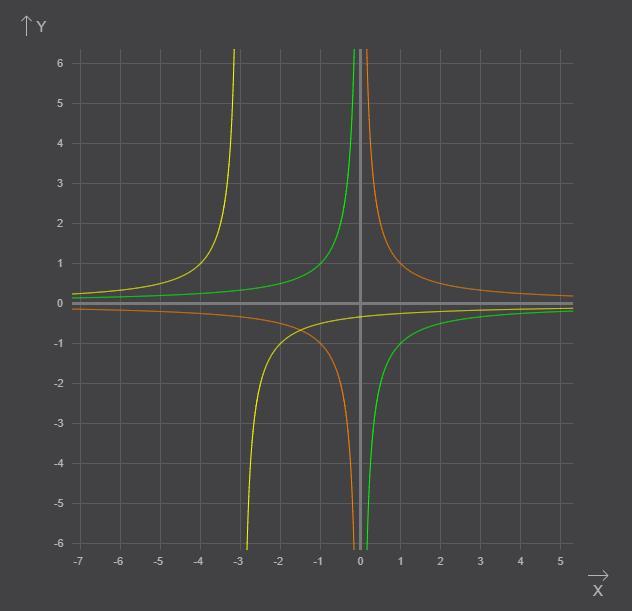
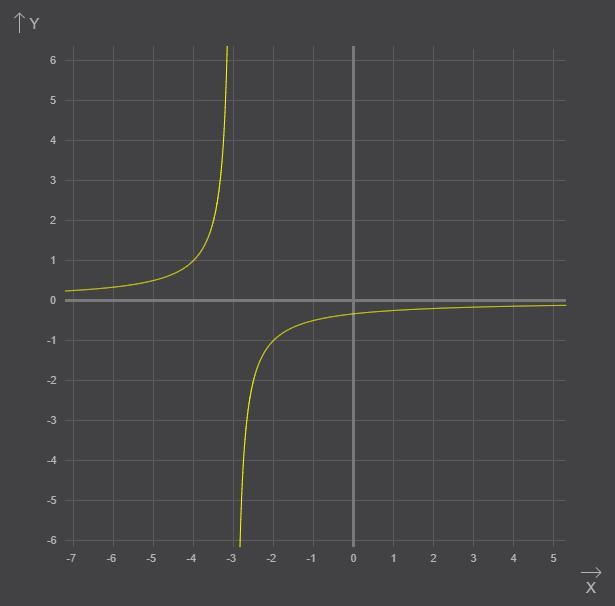
Строим график функции $y=\dfrac{1}{x}$ (оранжевый); отражаем его симметрично оси x (зеленый) и переносим на 3 единицы влево (желтый). Получим график функции $y=-\dfrac{1}{x+3}$.

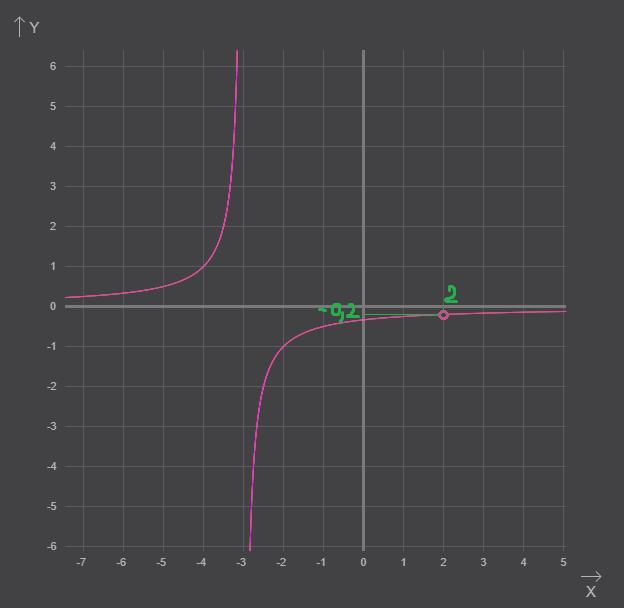
Однако, этот график не является графиком исходной функции, так как у функции $y=-\dfrac{1}{x+3}$ и у исходной функции различаются области определения.

Точка $x=-3$ не входит в область определения обеих функций.

Точка $x=2$ не входила в область определения исходной функции, но входит в область определения полученной функции $y=-\dfrac{1}{x+3}$. Нам нужно исключить ее из области определения полученной функции. Чтобы показать это графически, нам нужно выколоть из графика точку с абсциссой $x=2$.

Можем определить ординату этой точки:

$y=-\dfrac{1}{2+3} =-\dfrac{1}{5} =-0.2$

Определяем область значений функции. Функция может принимать любые значения, кроме двух: 0 и -0.2.

$y=0$ - соответствует асимптоте функции

$y=-0.2$ - соответствует выколотой точке

Таким образом:

$E(y)=(-\infty;\ -0.2)\cup(-0.2;\ 0)\cup(0;\ +\infty)$