Question

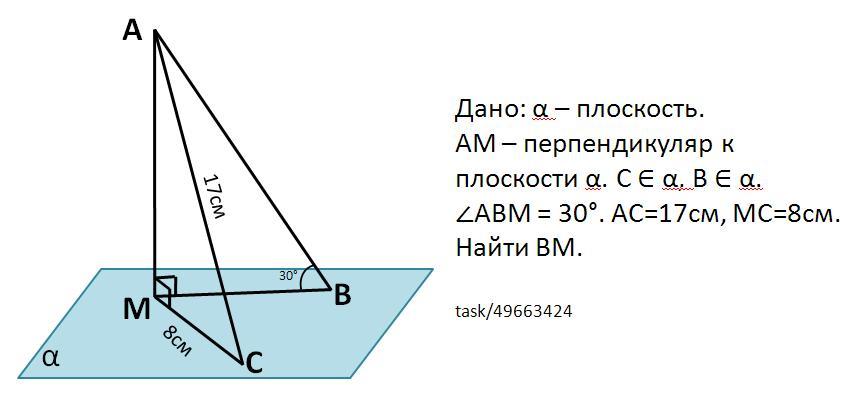
Из точки А опущен перпендикуляр АМ на плоскость α, точки В и С принадлежат плоскости α, АС=17см, МС=8см, угол АВМ=30. Найти ВМ.Срочно!

Answer 1

Из точки А опущен перпендикуляр АМ на плоскость α, точки В и С принадлежат плоскости α, АС=17см, МС=8см, угол АВМ=30°. Найти ВМ.

Ответ:

MB = 15√3 см.

Объяснение:

• Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой, лежащей в этой плоскости.

AM⊥α, ВM ∈ α и MC ∈ α ⇒ AM⊥BM, AM⊥МС.

• Треугольник называют прямоугольным, если у него есть две взаимно перпендикулярные стороны.

AM⊥BM, AM⊥МС ⇒ ΔАМВ и ΔАМС - прямоугольные.

Рассмотрим ΔАМС - прямоугольный.

• Теорема Пифагора: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

АС - гипотенуза, АМ и МС - катеты, АС=17см, МС=8см

$\Large \boldsymbol {} \hookrightarrow AC^2=MC^2+AM^2 \Longrightarrow AM=\sqrt{17^2-8^2}=\\\\=\sqrt{289-64} = \sqrt{225}=15$

AM=15см.

Рассмотрим ΔАМB - прямоугольный.

• Тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему.

$\Large \boldsymbol {} \hookrightarrow \text{tg}\ \angle AMB = \frac{AM}{MB} \Longrightarrow MB=\frac{AM}{\text{tg}\ \angle AMB} =\frac{15}{\text{tg}\ 30^\circ} =\\\\=15 \div \frac{\sqrt{3} }{3} =\frac{45 }{\sqrt{3} }*\frac{\sqrt{3} }{\sqrt{3} } =\frac{\not45\stackrel{15}{*}\sqrt{3} }{\not3} =15\sqrt{3}$

MB = 15√3 см.