ДОПОМОЖІТЬ ЦЕ ТЕРМІНОВО
завдання: дослідити функцію на екстремуми
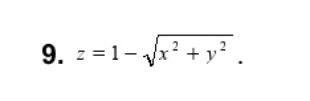
Ответы
Ответ:
точка М₀(0; 0) - точка максимума по определению
fmax = 1
Пошаговое объяснение:
Если мы пойдем обычным путем исследования функции на экстремумы, т.е. найдем частные производные и будем искать стационарные точки, то мы столкнемся с неприятным случаем.
Вот посмотрим.
Частные производные.
приравняем их к нулю
эта система не имеет решений, т.r одновременное равенство 0 переменных х и у приводит к равенству yek. знаменателя.
И вот вроде как функция в точке (0; 0) не дифференцируема.
Но сама же функция в этой точке определена и соответствующая поверхность в этой точке непрерывна.
И более того, в знаменателе частных производных второго порядка так же будет фигурировать в знаменателе, что не даст возможности проверить достаточное условие наличия экстремума.
В таком случае нужно рассмотреть точки предполагаемого экстремума в разрезе их определения.
Рассмотрим достаточно малую -окрестность точки M₀(0;0). Любую точку данной окрестности, отличную от M₀, можно представить в виде M(0+Δx; 0+Δy), где значения Δx и Δу не равны нулю одновременно и достаточно малы для того чтобы точка входила в эту окрестность.
(Δx и Δу могут быть как положительными, так и отрицательными, и могут быть разных знаков.)
Значение функции в точке М
Корень из квадратов "дельт" пусть хоть чуть-чуть, но больше нуля.
Поэтому, если f(M₀) = 1, будет вполне справедливо написать, что
f(M) < f(M₀).
Таким образом, у нас для точки М₀(0; ) нашлась окрестность, такая, что в ее пределах выполняется неравенство f(M) < f(M₀).
Следовательно, точка М₀ (0; 0) - точка максимума по определению.
Максимум функции fmax = 1.
#SPJ1