Предмет: Алгебра,
автор: kk7718790
Помогите алгебра 9 класс
Приложения:
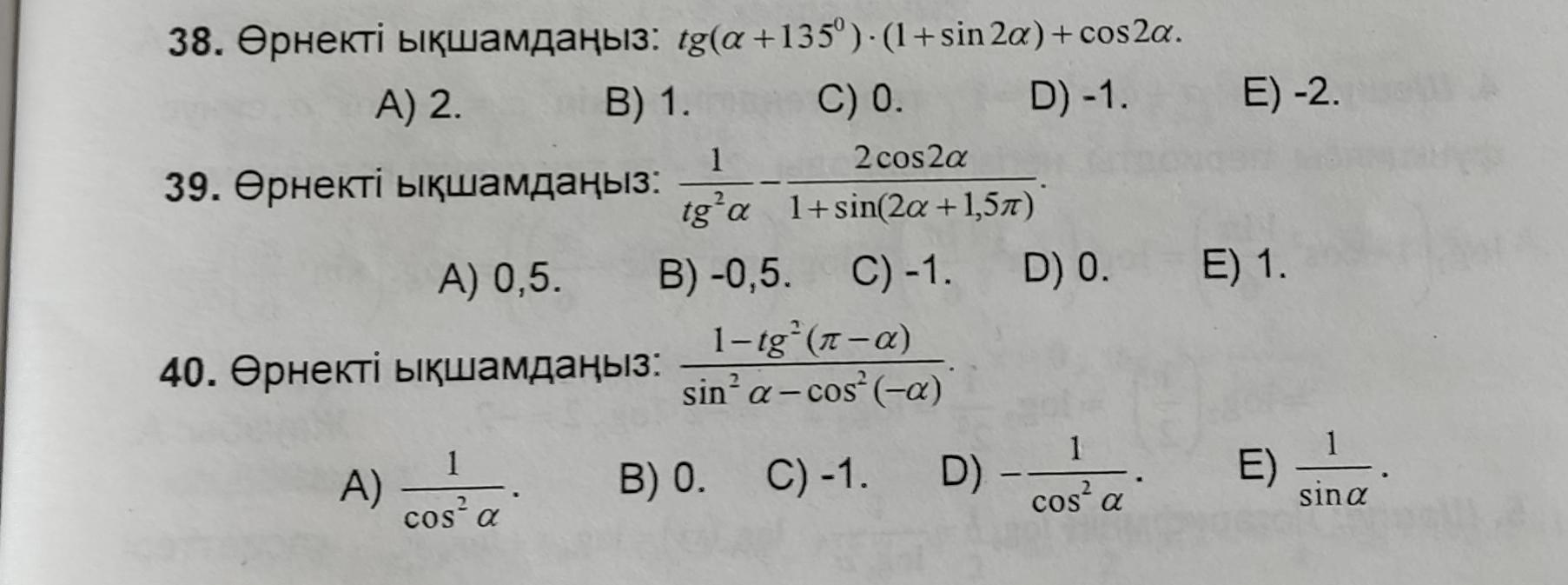
Ответы
Автор ответа:
1
Ответ:
Применяем формулы приведения, формулы двойных углов .
Ответ: С) .
Ответ: Е) .
Ответ: D) .
Похожие вопросы
Предмет: Окружающий мир,
автор: sevdaismaiylova
Предмет: Русский язык,
автор: KROXSI
Предмет: Русский язык,
автор: KekNeKek
Предмет: Русский язык,
автор: violetzhigareva
Предмет: Математика,
автор: nelenecz