Question

Даю 40 БАЛОВ, очень нужно, прошу

Answer 1

Ответ:

$\displaystyle \boldsymbol {BD=4\sqrt{21} }$

Пошаговое объяснение:

1) делаем  чертеж  (рис 1)

AS = 10 cм

SE = 6 см

∠SEA = 90°

по теореме Пифагора

$\displaystyle AE =\sqrt{(AS)^2-(SE)^2} =\sqrt{10^2-6^2} =\sqrt{64} =8$ (см)

Тогда диагональ квадрата

АС = 2АЕ = (8см *2) = 16 см

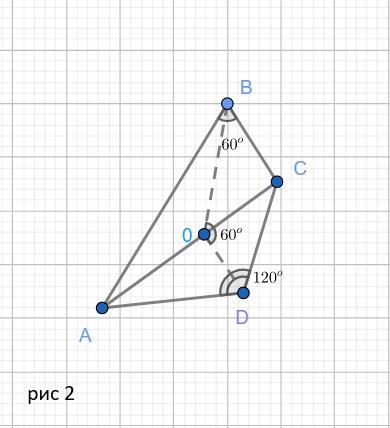
2) чертеж на рис 2

ΔАВС  равнобедренный.

∠ABC = 60°, следовательно ΔАВС - равносторонний.

АВ = 24 см

ВО в равностороннем треугольнике и высота, и медиана, и биссектриса.   ⇒  АО = 12см

ΔАВО :

$\displaystyle OB=\sqrt{(AB)^2-(AO)^2} =\sqrt{24^2-12^2} =\sqrt{432} =\underline {12\sqrt{3} }$

ΔAOD  - равнобедренный, высота = биссектриса :

∠ODA =  120° : 2 = 60°

$\displaystyle \frac{AO}{OD} =tg(60^o)=\sqrt{3} \\\\\\OD=12:\sqrt{3} =\frac{12}{\sqrt{3} } =\frac{12*\sqrt{3} }{\sqrt{3} *\sqrt{3} }=\underline {4\sqrt{3} }$

И теперь из треугольника BOD по теореме косинусов вычисляем BD

∠BOD = 60° по условию.

BD² = (OB)² +(OD)²-2OB*OD*cos(60°) =

       = 432  + 16*3  - 2*(12√3) * (4√3) *cos(60°) =

       = 432  + 48    -  2*12*4*3*0.5 = 336

$\displaystyle \boldsymbol {BD=\sqrt{336} =\sqrt{16*21} =4\sqrt{21} }$

#SPJ1