Question

Розв'яжiть графiчно систему:

{y+x=0
{4x+y= 6​

Answer 1

Ответ:

$\displaystyle \boldsymbol {\left \{ {{y=-2} \atop {x=2\hfill}} \right. }$

Объяснение:

Система уравнений

$\displaystyle \left \{ {{x+y=0} \atop {4x+y=6}} \right. \left \{ {{y=-x\hfill} \atop {y=6-4x}} \right.$

Для обоих уравнений графики - прямые линии.

Любая прямая строится по двум точкам.

а)  у = -х

Прямая, проходящая через начало координат.

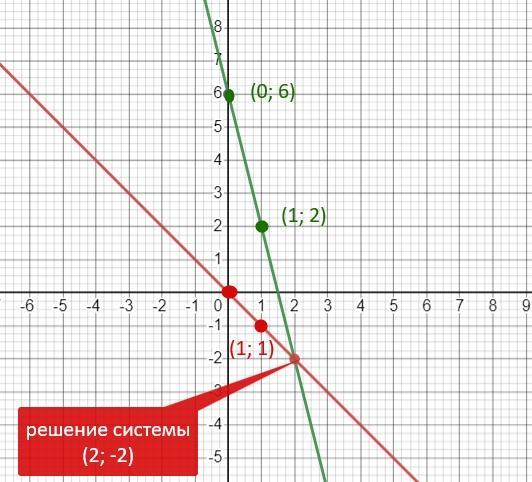
Одна точка    :                             (0; 0)

Другая точка:  х = 1;  у = -1   ⇒   (1; -1)

b) у = 6 - 4х

Одна точка:     х = 0;  y = 6 - 4*0 = 6     ⇒ (0; 6)

Другая точка:  x = 1;   y = 6 - 4*1 = 2      ⇒ (1; 2)

Теперь строим два графика и точка их пересечения будет решением системы.

Точка пересечения графиков (2; -2)

Решение системы     $\displaystyle \left \{ {{y=-2} \atop {x=2\hfill}} \right.$