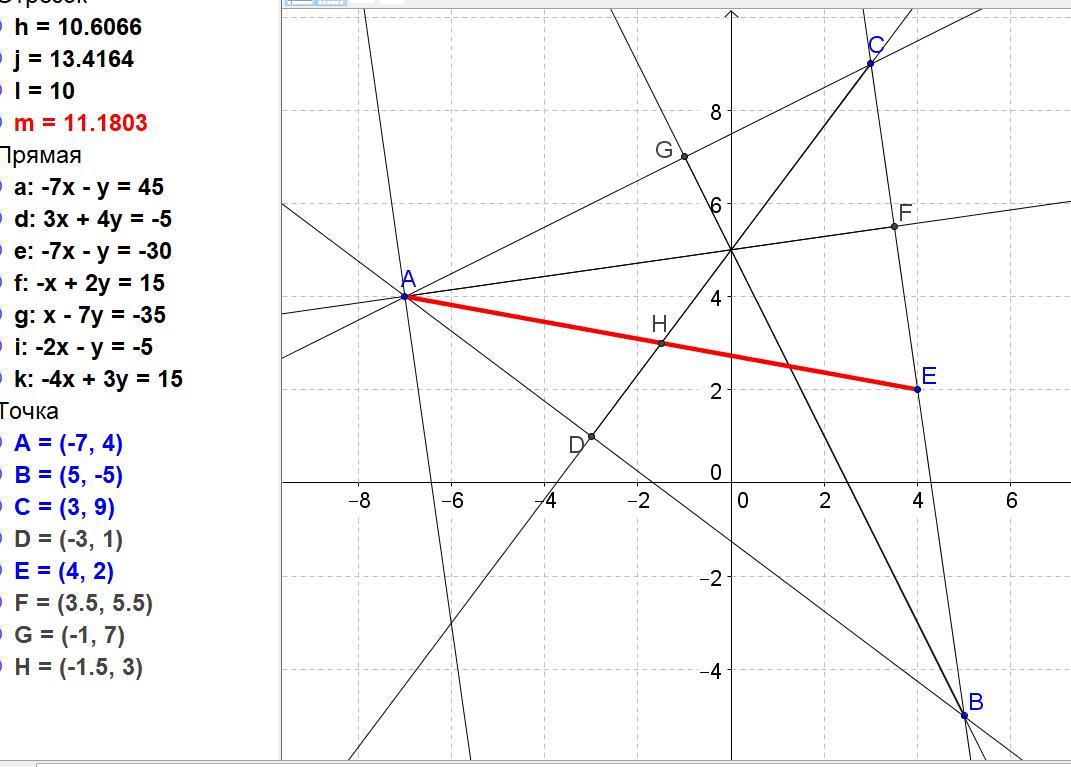
Дані координати вершин трикутника АВС А(-7;4) В(5;-5) С(3;9). Знайти: 1) довжину сторони АВ; 2) рівняння сторін АВ і ВС і їх кутові коефіцієнти; 3) кут В в радіанах; 4) рівняння висоти СД і її довжину; 5) рівняння медіани АЕ; 6) координати точки перетину медіани АЕ і висоти СД; 7) рівняння прямої, що проходить через точку А, паралельно прямій ВС. Зробити малюнок.
Ответы
Дані координати вершин трикутника АВС А(-7;4) В(5;-5) С(3;9). Знайти:
1) довжину сторони АВ;
Вектор АВ = (5-(-7); -5-4) = (12; -9).
Его модуль равен
|AB| = √(12² + (-9)²) =√(144 + 81) = √225 = 15.
2) рівняння сторін АВ і ВС і їх кутові коефіцієнти;
Уравнение стороны АВ определяем по найденному вектору АВ (12; -9) и точке А(-7; 4).
AB: (x + 7)/12 = (y – 4)/(-9),.
-9x – 63 = 12y – 48,
9x + 12y + 15 = 0 или, сократив на 3:
3x + 4y + 5 = 0.
Находим вектор ВС.
ВС = (3-5; 9-(-5)) = (-2; 14).
Его модуль равен
|ВС| = √((-2)² + 14²) =√(4 + 196) = √200 = 10√2.
BC: (x - 5)/(-2) = (y + 5)/14,.
14x – 70 = -2y – 10,
14x + 2y - 60 = 0 или, сократив на 2:
7x + y - 30 = 0.
3) кут В в радіанах;
ВА = -АВ = (-12; 9),
|AB| = 15.
ВС = (-2; 14).
|ВС| = 10√2.
cos B = (-12*(-2) + 9*14)/(15*10√2) = 150/150√2 = 1/√2.
Угол В равен:
B = arccos(1/√2) = 0,785398163 радиан или 45 градусов.
4) рівняння висоти СD і її довжину;
Высота СD – это перпендикуляр к прямой АВ 3x + 4y + 5 = 0 из точки С(3; 9).
Прямая, проходящая через точку M1(x1; y1) и перпендикулярная прямой Ax+By+C=0, представляется уравнением
A(y-y1)-B(x-x1)=0.
Подставим данные и получаем уравнение высоты СD:
3(y – 9) – 4(x - 3) = 0 или 4x – 3y + 15 = 0.
5) рівняння медіани АЕ;
Находим координаты точки Е как середину отрезка ВС.
Е = (В(5; -5 + С(3; 9)) / 2 = (4; 2).
Вектор АЕ = Е(4; 2) - А(-7; 4) = (11; -2).
Находим уравнение медианы АЕ по точке А(-7; 4) и вектору АЕ(11; -2).
Уравнение АМ: (х + 7)/11 = (у - 4)/(-2).
-2x – 14 = 11y - 44
2x + 11y - 30 = 0.
6) координати точки перетину медіани АЕ і висоти СД;
AE: 2x + 11y - 30 = 0 |x(-2) = -4x - 22y + 60 = 0
СD: 4x – 3y + 15 = 0 4x – 3y + 15 = 0
-25y + 75 = 0
y = -75/-25 = 3,
x = (-11y + 30)/2 = (-11*3 + 30)/2 = -1,5.
Точка Н(-1,5; 3).
7) рівняння прямої, що проходить через точку А, паралельно прямій ВС.
Её уравнение с коэффициентами как у прямой ВС 7x + y + С = 0.
Подставим координаты точки А(-7; 4).
7*(-7) + 4 + С = 0.
С = 49 – 4 = 45.
Получаем 7x + y + 45 = 0.