Предмет: Алгебра,
автор: nnmgbpk533
найти n, если...

Приложения:
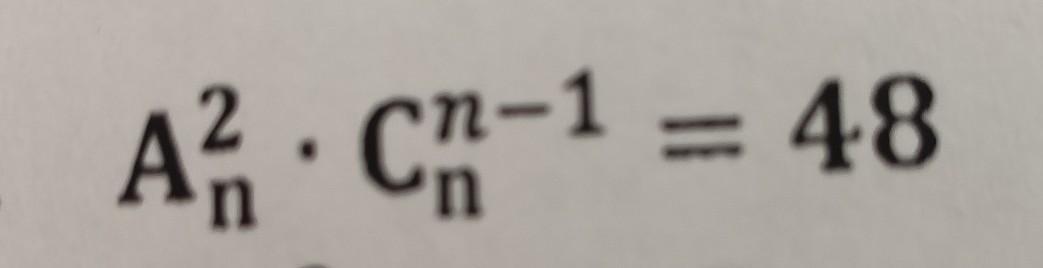
nnmgbpk533:
была опечатка, в конце 48n², уже нашел ответ
Ответы
Автор ответа:
0
Ответ:
Формулы: .
Похожие вопросы
Предмет: Русский язык,
автор: snegovik4
Предмет: Українська мова,
автор: Dimonrik
Предмет: Русский язык,
автор: zemer1
Предмет: Биология,
автор: Mamaolga1