Предмет: Математика,
автор: galoyangohar2
помогите решить упражнение
Приложения:
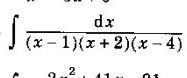
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Эту задачу можно решить стандартным способом, разложив подинтегральную функцию на элементарные дроби, скажем, с помощью неопределенных коэффициентов. Но мы попробуем упростить выкладки, сделав замену x-1=t; dx=dt. Получаем интеграл
. замена t²=p приводит к интегралу
Усредняющая замена
сводит интеграл к табличному:
Похожие вопросы
Предмет: Английский язык,
автор: мичман1йфя
Предмет: Русский язык,
автор: alenyurina2016
Предмет: Окружающий мир,
автор: bege1986
Предмет: Алгебра,
автор: afanasevanatal
Предмет: Математика,
автор: ppppppppppp89