Предмет: Геометрия,
автор: ashamavos13
ДАЮ 40 БАЛЛОВ!!!!
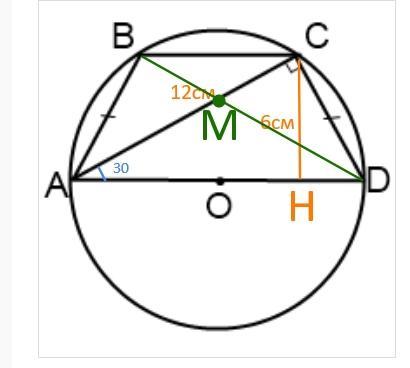
Навколо трапеції з висотою 6 см описано коло. Кут між радіусами кола, проведеними до кінців бічної сторони, дорівнює 60°. Знайдіть площу трапеції.
Ответы
Автор ответа:
1
Ответ:
см²
Объяснение:
1. вписать в окружность можно только равнобокую трапецию.
2. вписанный угол равен половине соответствующего ему центрального угла.
Исходя из этого, мы можем найти диагональ трапеции.
∠COD = 60° по условию
∠CAD = 30° как вписанный, опирающийся на дугу в 60°.
Тогда из ΔACH находим гипотенузу. Она равна удвоенному катету, лежащему против угла в 30°.
АС = 12см.
Площадь трапеции равна через диагонали
В равнобедренном треугольнике AMD углы при основании равны, они по 30°.
Тогда угол между диагоналями равен
∠AMD = 180° - 2*30° = 120°
Тогда площадь трапеции
На рисунке центр окружности лежит на основании трапеции. Это получается по углам. но на решение это не влияет, поэтому доказывать, где лежит центр не надо.
Приложения:
ashamavos13:
Огромное вам спасибо! Пол вечера сидела, вы очень подробно объяснили!
пожалуйста. рада что помогла. -))
Похожие вопросы
Предмет: Русский язык,
автор: 333Света333
Предмет: Русский язык,
автор: AnnaMashtaler
Предмет: Английский язык,
автор: СветланаСветик3
Предмет: Биология,
автор: kira7885
Предмет: Литература,
автор: Antiloh