Предмет: Алгебра,
автор: dreyfarrion
Помогите пж срочно......
Приложения:

Ответы
Автор ответа:
1
Ответ:
x = 1
Объяснение:
Приложения:
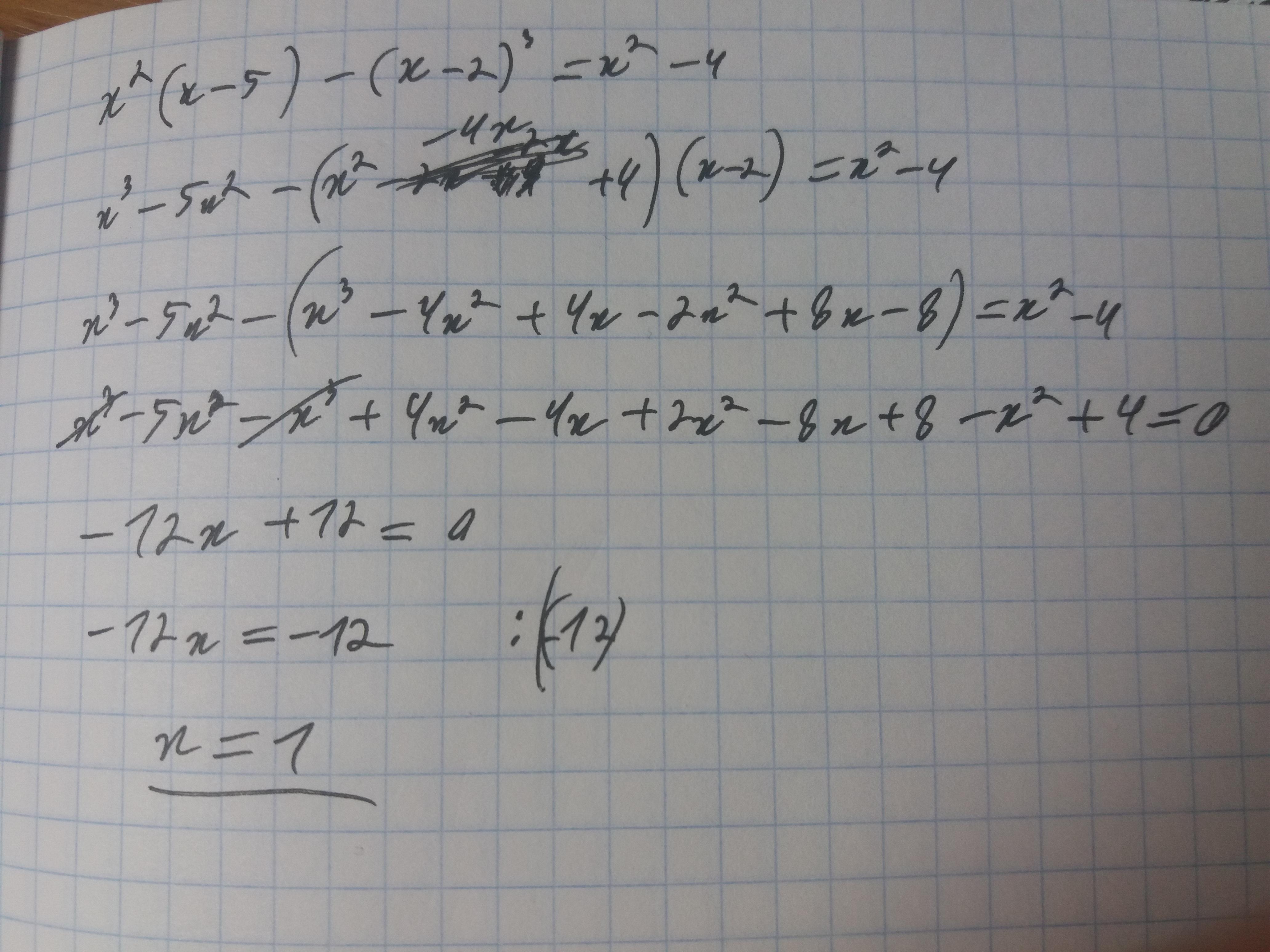
Автор ответа:
1
Ответ:
Объяснение:
Получаем 2 корня:
Похожие вопросы
Предмет: Русский язык,
автор: Di1114
Предмет: Русский язык,
автор: ryff1
Предмет: Русский язык,
автор: Bestlera
Предмет: Математика,
автор: 79780063821
Предмет: Математика,
автор: 69698767a4