Предмет: Геометрия,
автор: Аноним
Точка дотику вписаного кола рiвнобедреного трикутника ділить його бічну сторону у відношенні 7 : 4, рахуючи від вершини трикутника. Знайдіть сторони трикутника, якщо його периметр дорівнює 120 см.
zmeura1204:
7+4=11 частей боковая сторона 4*2=8 частей основание. 120/(11+11+8)=120/30=4; 4*11=44 боковая сторона; 8*4=32 основание.
спасибо
у меня в профиле есть ещё задания
буду рада если поможете
Ответы
Автор ответа:
0
Ответ:
44 см, 44 см, 32 см
Объяснение:
Дано: ΔАВС, АВ=ВС; ВК:АК=7:4, Р=120 см. АВ, ВС, АС - ?
Відрізки дотичних, проведені до кола з однієї точки, рівні між собою.
АК=АМ=4х см; СМ=СТ=4х см; ВК=ВТ=7х см.
АВ=ВС=4х+7х=11х см; АМ=СМ=4х+4х=8х см
11х+11х+8х=120
30х=120; х=4
АВ=ВС=11*4=44 см, АС=8*4=32 см.
Приложения:
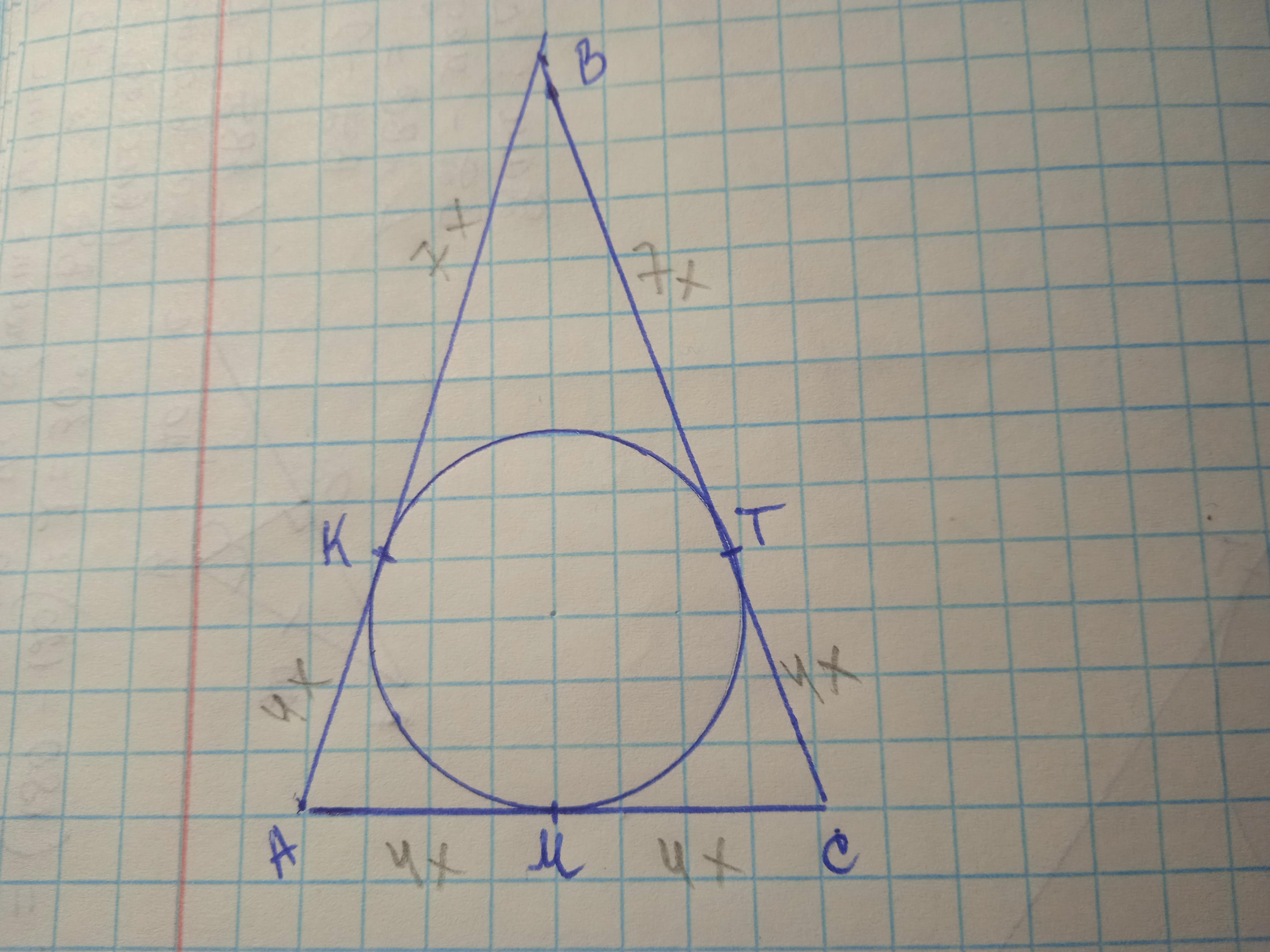
Похожие вопросы
Предмет: Қазақ тiлi,
автор: diasosmanov
Предмет: Английский язык,
автор: interest2
Предмет: Қазақ тiлi,
автор: Мария0009
Предмет: Физика,
автор: polshkovkol11
Предмет: Английский язык,
автор: vika0289111