Предмет: Алгебра,
автор: sefiteni
решите пж СРОЧНО!!!!!!!! очень надо
Приложения:
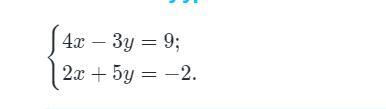
Ответы
Автор ответа:
1
Ответ:
(см. объяснение)
Объяснение:
Способ 1:
Способ 2:
Способ 3:
- базисные.
Графический и вариации школьных аналитических способов опускаю.
Система уравнений решена!
Похожие вопросы
Предмет: Английский язык,
автор: viktoriya129
Предмет: Русский язык,
автор: selenekova2004
Предмет: Английский язык,
автор: veraatabaeva11
Предмет: Химия,
автор: artyom55554
Предмет: Литература,
автор: Plu9