Question

Помогите пожалуйста срочно прошу дам 40 балов

Answer 1

$\displaystyle\bf\\\Big(x+y-2c\Big)\Big(y-x\Big)-\Big(y+c-2x\Big)\Big(y-c\Big)+\Big(c+x-2y\Big)\Big(x-c\Big)+13=\\\\=xy-x^{2} +y^{2} -xy-2cy+2cx-y^{2} +cy-cy+c^{2} +2xy-2cx+\\\\+cx-c^{2}+x^{2} -cx-2xy+2cy +13=\underbrace{\Big(-x^{2} +x^{2} \Big)}_{0}+\underbrace{\Big(y^{2}-y^{2}\Big)}_{0} +\\\\+\underbrace{\Big(c^{2}-c^{2} \Big)}_{0}+\underbrace{\Big(xy-xy+2xy-2xy\Big)}_{0}+\underbrace{\Big(2cx-2cx+cx-cx\Big)}_{0}+\\\\+\underbrace{\Big(2cy-2cy+cy-cy\Big)}_{0}+13=13$

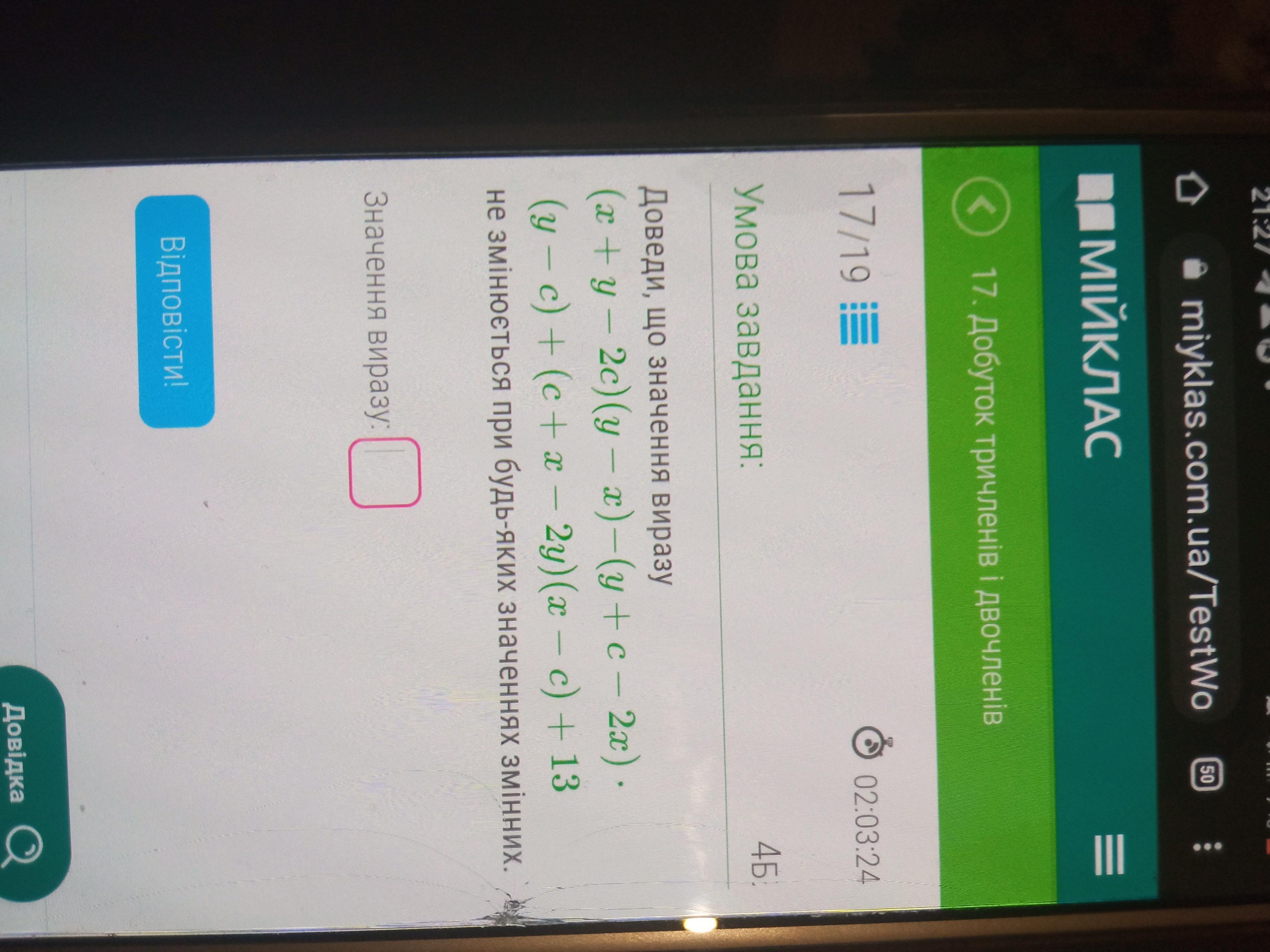
После упрощения выражения получили ответ , в котором не содержится ни одной переменной , значит значение выражения не изменится , так как не зависит от значения переменных .