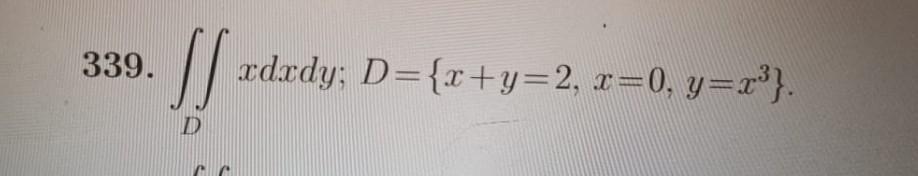Решить интеграл..........
Приложения:
Ответы
Объяснение:


Похожие вопросы
!!! ПОМОГИТЕ !!!
Задание № 1: вставьте в прилагательные пропущенные буквы, объясните написание:
(1) На дальн… острове; (2) за свеж…м хлебом; (3) в дремуч…м лесу; (4) в жгуч… крапиву; (5)на д…леком ра(с,сс)тояни…; (6) предутренн…м ветерком; (7) на пр…школьн…м участке; (8)в пр…брежной зелен…; (9) причудлив… узора; (10) пр…огромн…й сыроежки.
Задание № 2: заполните таблицу «Способы образования имен прилагательных»; выделите морфему, с помощью которой образовано прилагательное:
Приставочный
Суффиксальный
Приставочно-суффиксальный
Сложение основ
Сложение слов
(1) Премудрый, (2) безопасный, (3) бесхозяйственный, (4) весенний, (5) матросский, (6)серебристый, (7) безупречный, (8) заморский, (9) надземный, (10) русско-английский, (11)сельскохозяйственный, (12) труднодоступный, (13) вечнозеленый, (14) осенний, (15)водный, (16) безветренный, (17) наручный, (18) подводный, (19) городской, (20) гористый,(21) бесстрашный, (22) привокзальный, (23) приветливый, (24) высокоточный,
Задание № 3: запишите по образцу рядом с полной формой прилагательных краткую; у прилагательных выделите окончания и определите род:
Образец: интересный – интересен (муж. р.), интересна (жен. р.), интересно (ср. р.).
(1) Честный, (2) забавный, (3) редкий, (4) чистый, (5) уютный, (6) сладкий, (7) темный.
Задание № 4: подберите антонимы к данным кратким прилагательным; выделите окончания:
Образец: умен – глуп.
(1) Нежен, (2) печален, (3) сердит, (4) горяч, (5) весел, (6) решителен.
Задание № 5: преобразуйте предложения по образцу:
Образец: Ситец линяет. – Ситец линюч.
(1) Напиток шипит. (2) Мороз трещит. (3) Цветок пахнет. (4) Ветер жжет. (5) Бензин горит.
Задание № 6: спишите, подчеркните прилагательные как члены предложения; назовите антонимы:
Полюбил богатый – бедную, / Полюбил ученый – глупую, / Полюбил румяный – бледную, / Полюбил хороший – вредную; / Золотой – полушку медную.
(М. И. Цветаева)
Задание № 7: подчеркните грамматические основы; выделите суффиксы прилагательных, определите их степень сравнения:
«Я ль, скажи мне, всех милее, / Всех румяней и белее?» / Что же зеркальце в ответ? / «Ты прекрасна, спору нет; / Но царевна всех милее, /Всех румяней и белее». <…> «Ах ты, мерзкое стекло! / Это врёшь ты мне назло. <…> / Признавайся: всех я краше. / Обойди всё царство наше, / Хоть весь мир; мне ровной нет. / Так ли?» / Зеркальце ж в ответ: / «А царевна всё ж милее, / Всё ж румяней и белее». (А. С. Пушкин).
Задание № 8: спишите, раскрывая скобки, объясняя слитное и раздельное написание слов разных частей речи с частицей «не»:
(1) (Не)заслонишь солнышка рукавицей, (не)убьешь молодца небылицей. (2) Кукушка (не)ястреб, а (не)уч (не)мастер. (3) (Не)ряха всегда полдела делает. (Пословицы). (4) Вдали были видны (не)ясные очертания неба. (5) Погода в эту зиму (не)постоянная, а очень изменчивая.
Задание № 9: спишите¸ обозначая орфограмму № 37:
(1) Кварц…рас лампа, (2) парч…вый халат, (3) плеч…вой сустав, (4) груш…вый сок, (5)сторож…вой пост, (6) ерш…вые повадки, (7) морж…вый клык, (8) плюш…рас скатерть, (9)образц…вый порядок, (10) еж…вые рукавицы.
Задание № 10: выпишите слова в две колонки: 1) существительные с буквами «о», «е» после шипящих в суффиксах; 2) прилагательные с буквами «о», «е» после шипящих в суффиксах:
(1) Ситц…вый, (2) бельч…нок, (3) холщ…вый, (4) овраж…к, (5) снеж…к, (6) пятач…к, (7)луч…вой, (8) галч…нок, (9) замоч…к, (10) свинц…вый, (11) песц…вый, (12) ножич…к, (13)ландыш…вый, (14) зайч…нок, (15) молодц…ватый, (16) медвеж…нок.
Задание № 11: вставьте в прилагательные пропущенные буквы, объясните написание; суффиксы выделите:
(1) Конституцио…ый, (2) осе…ий, (3) тума…ый, (4) утре…ий, (5) пчели…ый, (6) деревя…ый, (7) журавли…ый, (8) раси…ый, (9) бессо…ый, (10) оловя…ый, (11) цели…ый, (12)огне…ый, (13) экскурсио…ый, (14) кожа…ый, (15) серебря…ый, (16) стекля…ый, (17)овся…ый.
Задание № 12: вставьте в прилагательные пропущенные буквы, объясните написание; суффиксы выделите:
(1) Матрос…ий, (2) близ…ий, (3) англий…ий, (4) немец…ий, (5) октябрь…ий, (6)пассажир…ий, (7) богатыр…ий.
Задание № 13: раскройте скобки, объясните написание сложных прилагательных:
(1) (Сельско)хозяйственный, (2) (физико)математический, (3) (русско)немецкий, (4)(стале)литейный, (5) (средне)вековый, (6) (туго)плавкий, (7) (зеленовато)серый, (8)(десяти)этажный, (9) (паровозо)ремонтный, (10) (юго)восточный, (11) (красный)красный,(12) (трех)метровый, (13) (садово)огородный, (14) (сорока)метровый, (15)(фабрично)заводской.