Предмет: Геометрия,
автор: ivanichceva
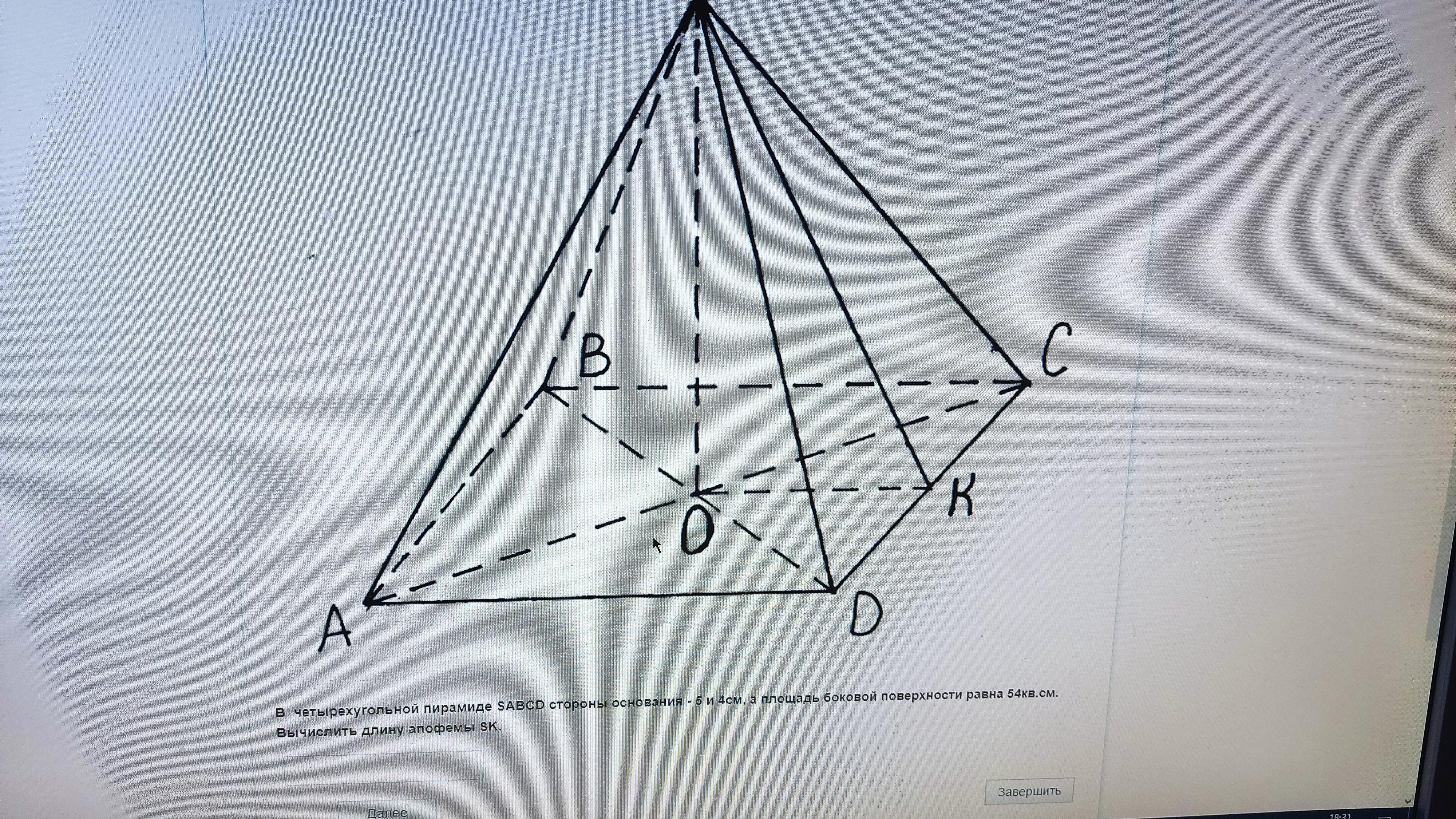
в четырехугольной пирамиде sabcd стороны основания 5 и 4 см а площадь боковой поверхности равна 54 кв.см . Вычислить длину апофемы SK
Приложения:
dnepr1:
В задании неточность: пирамида задана не правильная (стороны основания 5 м 4). По определению: апофема - это высота боковой грани ПРАВИЛЬНОЙ пирамиды.
Ответы
Автор ответа:
0
Sбок = 2*(1/2)*AD*SE + 2*(1/2)*CD*SK = AD*SE + CD*SK .
54 = 4* SE + 5*SK .
SE^2 = H^2 + (4/2)^2 = H^2 + 4
SK^2 = H^2 + (5/2)^2 = H^2 + 6,25.
54 = 4√(H^2 + 4) + 5√(H^2 + 6,25)
Решение этого уравнения даёт результат:
H=1/2 √(5863-480√143) ≈ 5,54605.
Отсюда находим искомое значение высоты SK боковой грани.
SK = √( H^2 + 6,25) = √( 30,75871083 + 6,25) = √37,00871083 = 6,083478514.
Похожие вопросы
Предмет: Русский язык,
автор: лера1525
Предмет: Английский язык,
автор: Аноним
Предмет: Другие предметы,
автор: Lolikc1
Предмет: Обществознание,
автор: sonya5718
Предмет: Математика,
автор: Аноним