Предмет: Алгебра,
автор: annsvet
Найдите производную функции, 20 баллов
Приложения:
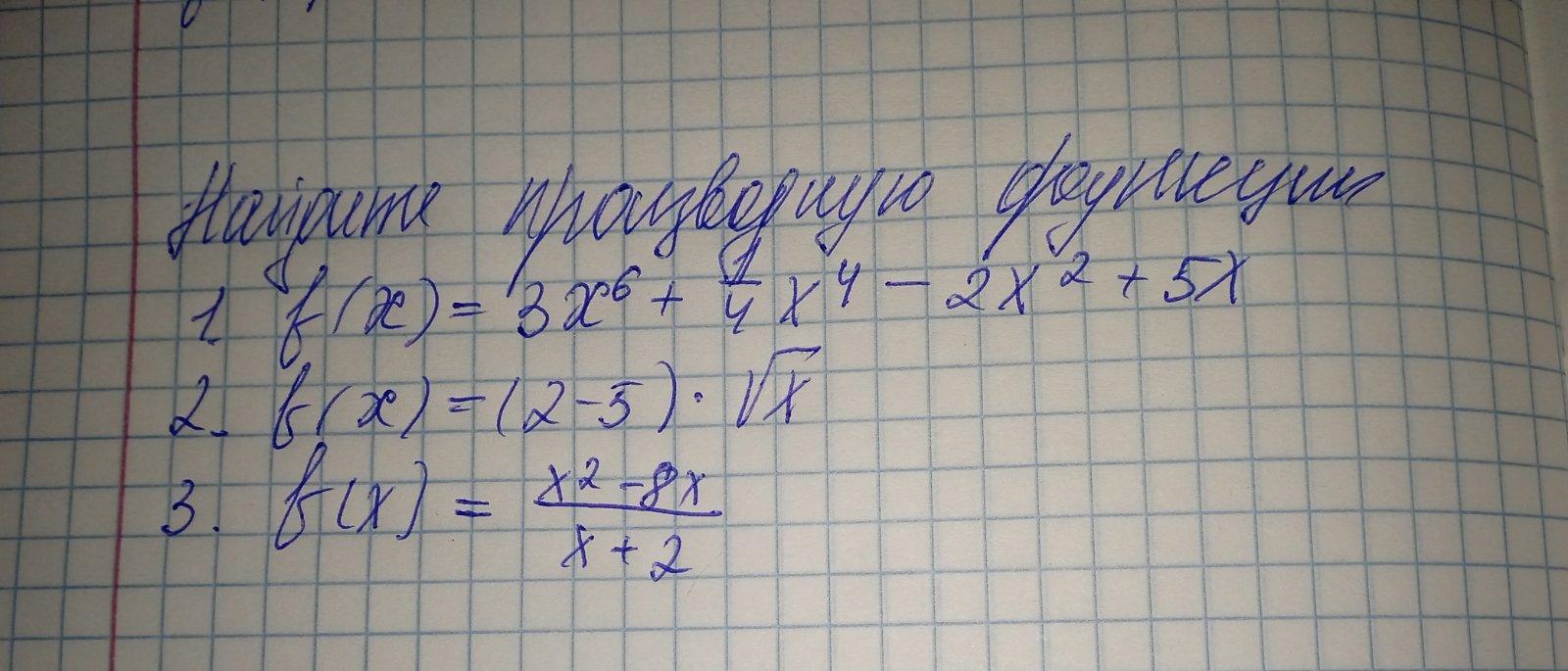
Ответы
Автор ответа:
0
Объяснение:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Lyusia1959
Предмет: Окружающий мир,
автор: kazancev222
Предмет: Алгебра,
автор: 555455591
Предмет: Русский язык,
автор: tarus73