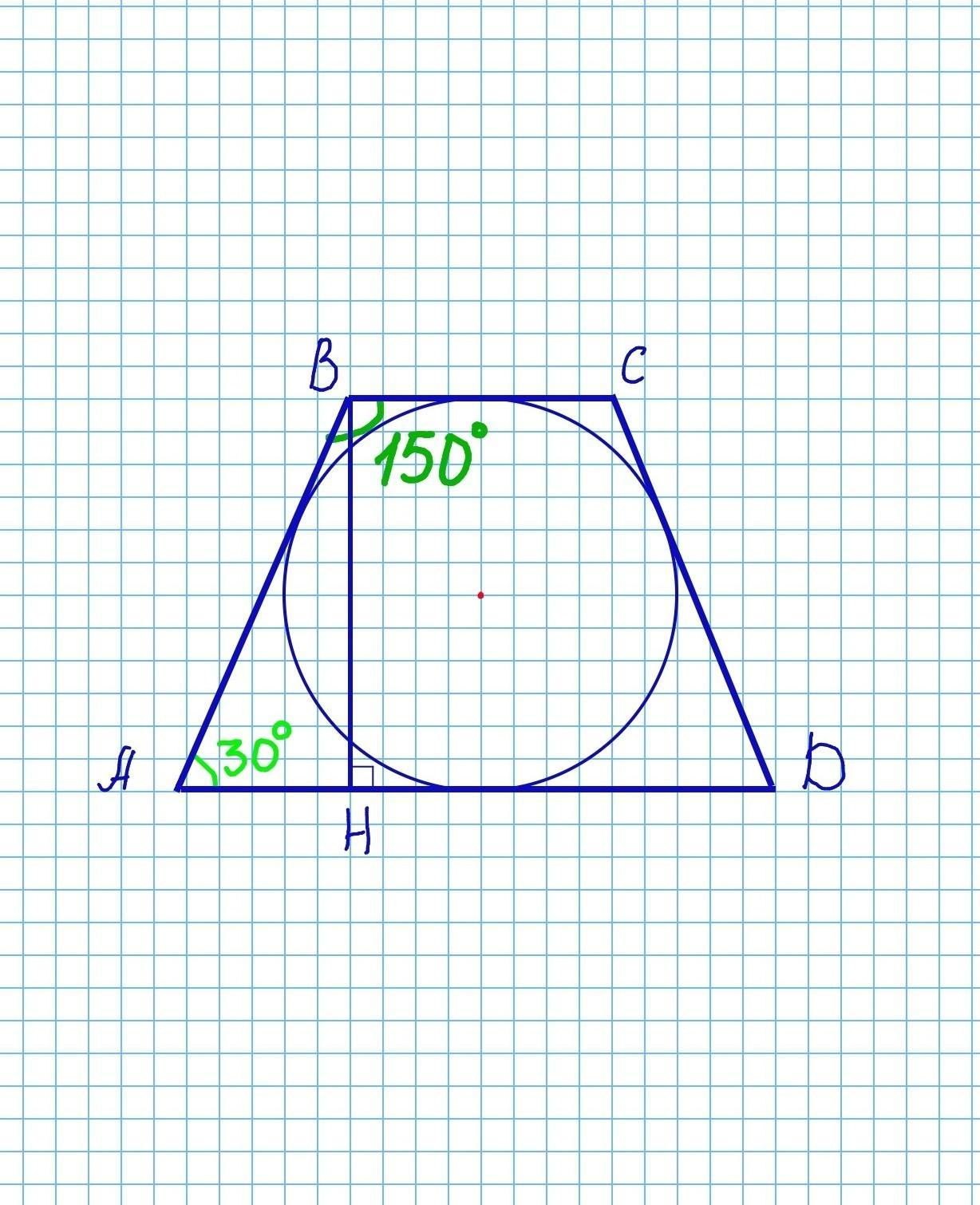
В равнобедренную трапецию с углом при основании 150° и
площадью 98 см2 вписана окружность радиуса . Найти .

Ответы
Ответ:
Радиус вписанной окружности равен 3,5 см
Объяснение:
В равнобедренную трапецию с углом ∠В=150° и площадью 98 см² вписана окружность радиуса r . Найти r.
- В трапецию можно вписать окружность тогда и только тогда, когда суммы её противоположных сторон равны.
AB + DC = AD + BC.
- Радиус вписанной в трапецию окружности равен половине её высоты.
Проведём высоту трапеции ВН. ВН⟂AD. Пусть BH = h.
Площадь трапеции равна полусумме её оснований умноженное на высоту:
S=½•(BC+AD)•h
Так как в трапецию можно вписать окружность, то BC+AD=AB+DC, соответственно площадь трапеции равна:
S=½•(AB+DC)•h
Рассмотрим прямоугольный △АВН.
Так как сумма углов, прилежащих к боковой стороне трапеции, равна 180 °, то
∠А=180°-∠В=180°-150°=30°.
Катет прямоугольного треугольника, лежащий напротив угла в 30° равен половине гипотенузы.Следовательно гипотенуза АВ=2•ВН=2h.
По условию АВСD - равнобедренная трапеция, а это значит, что её боковые стороны равны: CD=AB=2h.
Так как площадь трапеции равна 98 см², составим уравнение, найдём h.
½ • (2h + 2h) • h = 98
2h² =98
h² =49
h= √49
h=7 см.
Тогда радиус будет равен: r = ½•h = ½•7 = 3,5 см
#SPJ1