Предмет: Алгебра,
автор: kastryla49
Помогите прошу, очень срочно, дам 100 баллов
Приложения:
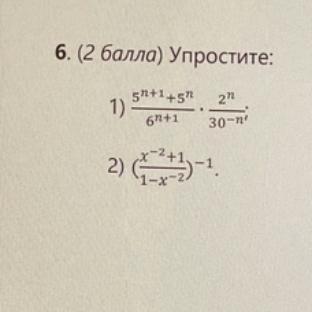
Ответы
Автор ответа:
1
Решение.
Применяем свойства степеней .
kastryla49:
спасибо большое , я очень рада, что вы ответили)
Похожие вопросы
Предмет: Русский язык,
автор: Полиночка365
Предмет: Русский язык,
автор: azersu1980
Предмет: Қазақ тiлi,
автор: La2riadarami
Предмет: Русский язык,
автор: Polya200986
Предмет: Математика,
автор: zuhrakimarme