Question

Можете бвтсро решить пожалуйста, отдам фулл баллы

В окружности проведены пересекающиеся хорды АВ и СD . Найдите m ( < DAC ) , если m ( < ACD ) = 40 " и m ( < ABC ) = 50 " .

Answer 1

Ответ:

∠DAC = 90°

Пошаговое объяснение:

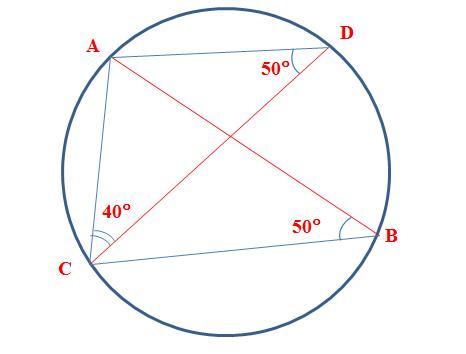
Дано (см. рисунок):

  AB и CD - пересекающийся хорды

  ∠ACD = 40°

  ∠ABC = 50°  

Найти: ∠DAC.

Решение.

Так как углы ABC и ADC опираются на дугу AC, то ∠ABC=∠ADC=50°.

Известно, что сумма внутренних углов треугольника равна 180°. Тогда для треугольника ADC верно равенство:

∠DAC + ∠ACD + ∠ADC = 180°.

Отсюда

∠DAC = 180° – ∠ACD – ∠ADC = 180° – 40° – 50° = 90°.

#SPJ1