Предмет: Математика,
автор: solka0000
Випадкова величина X задана функцією розподілу F(x). Знайти:
1) диф. функцію(густину ймовірності)
2) математичне сподівання
2) дисперсію
4)побудувати графіки інтегральної та диференціальної функції
Функція розподілу прикріплена на фото
Приложения:
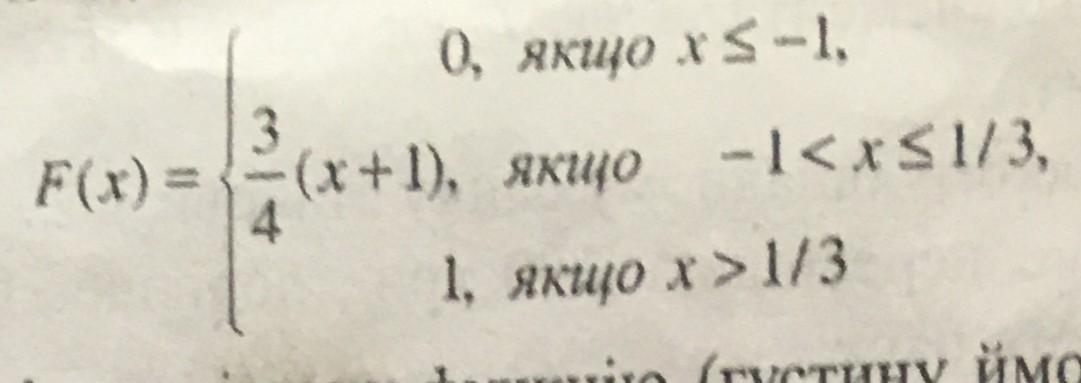
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Случайная величина X задана функцией распределения F(x). Найти:
1) Дифференциальную функцию (плотность вероятности).
2) Математическое ожидание.
2) Дисперсию.
4) Построить графики интегральной и дифференциальной функции.
Функция распределения прикреплена на фото.
1) Дифференциальная функция:
2)
Математическое ожидание:
3)
Дисперсия:
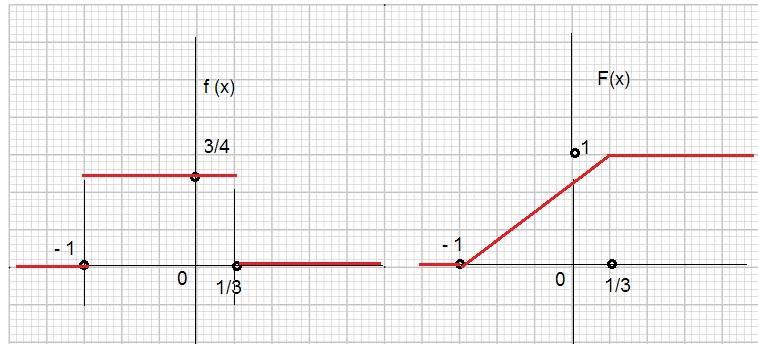
4) Графики:
Приложения:
solka0000:
в мене теж все так вийшло , коли я робила , але коли я шукала дисперсію ,то ще віднімала математичне сподівання в квадраті
дякую
Да, надо от 7/27 вычесть (-1/3)^2... D(X) = 20/27
добре ,ще раз дякую
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Katusha011
Предмет: Русский язык,
автор: sabik2005
Предмет: Математика,
автор: wwwso
Предмет: Русский язык,
автор: Аноним