Предмет: Математика,
автор: solka0000
МАТЕМАТИКА
ТЕРМІНОВО
ДОПОМОЖІТЬ ,БУДЬ ЛАСКА
розв'язати задачу Коші методом варіації сталої
(завдання на фото )
Приложения:
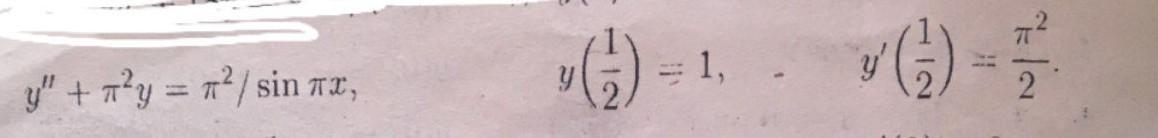
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
sangers1959:
Я решаю дальше.
Похожие вопросы
Предмет: Русский язык,
автор: victoriareih
Предмет: Русский язык,
автор: Марсель2488
Предмет: Русский язык,
автор: maydatd
Предмет: Другие предметы,
автор: dasha110906
Предмет: Английский язык,
автор: Kitti25