Question

помогите пожалуйста(
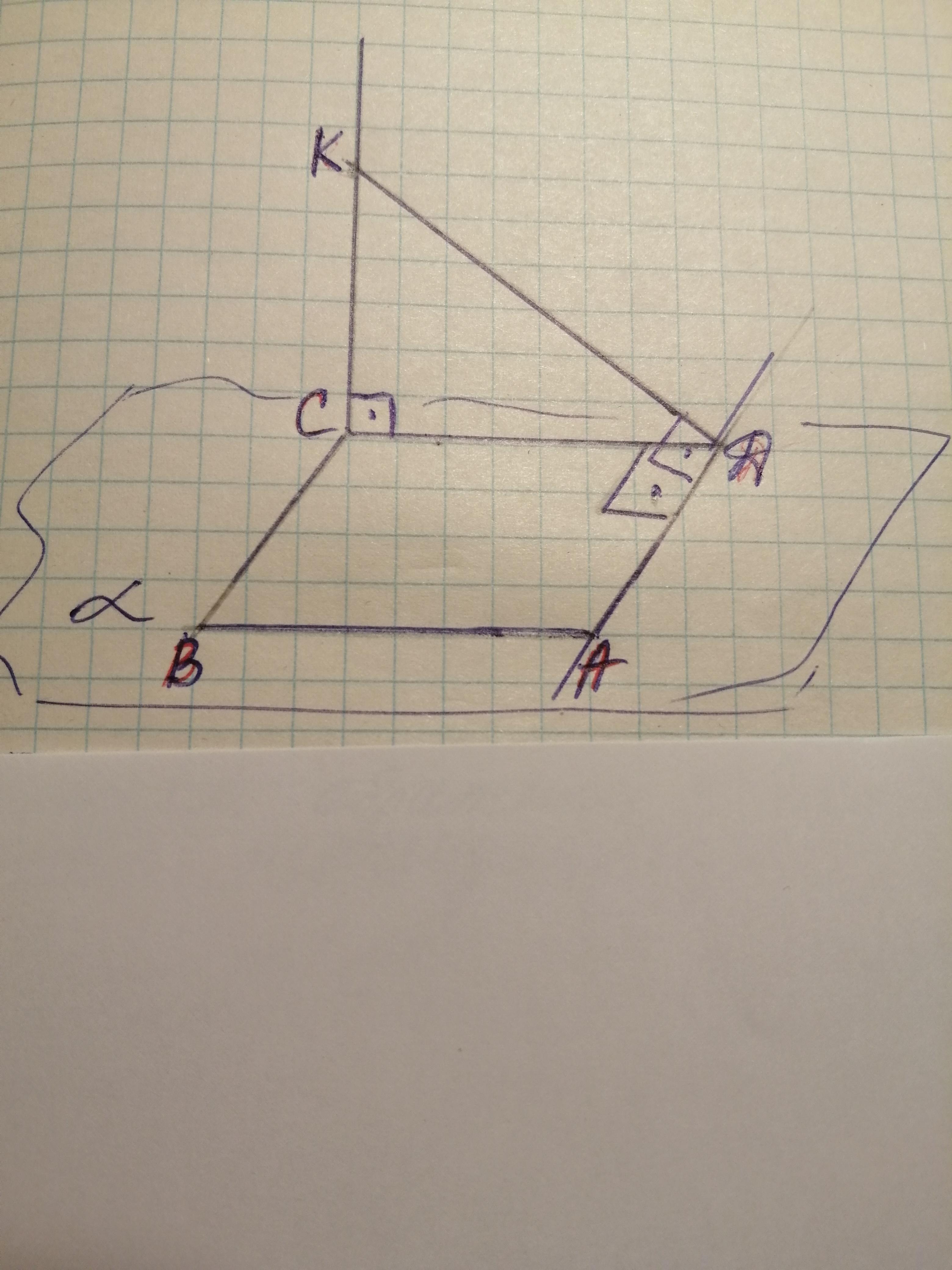
Через вершину С параллелограмма ABCD проведена прямая KC, перпендикулярная плоскости параллелограмма. Известно, что угол adk 90 °. Доказать что ABCD - прямоугольник (пожалуйста с дано, рисунком и решением )

Answer 1

Дано:

ABCD - параллелограмм, КС перпендикулярна плоскости параллелограмма, ∠ADK=90°

Доказать:

ABCD - прямоугольник

Доказательство:

1) AD лежит в плоскости параллелограмма ABCD

2) DK - наклонная к плоскости параллелограммa ABCD

3) ∠ADK=90° => DK ⊥ AD

4) CD - проекция наклонной DK

Следовательно, из п.п.1-4, по теореме обратной к теореме о трех перпендикулярах, AD ⊥ CD, т.е. ∠D=90°

5) ABCD - параллелограмм, следовательно, по свойству параллелограммам его противолежащие углы равны, значит

∠C = ∠D =90° (как противолежащие)

6)  Сумма углов параллелограмма, прилежащих к одной стороне, равна 180º. Значит, ∠D+∠C=180°

                                  90° + ∠C=180°

                                  ∠C = 180°-90°=90°

7) ∠A противолежит ∠С, следовательно, ∠А=90°

Итак, все углы параллелограмма прямые, значит параллелограмм ABCD является прямоугольником.

Что и требовалось доказать.

Теоема обратная к теореме о трех перпендикулярах:

"Если прямая на плоскости перпендикулярна наклонной к этой плоскости, то она перпендикулярна к проекции наклонной".