Предмет: Математика,
автор: Nekit10274
Помогите решить производную данной функции f(x)
Приложения:
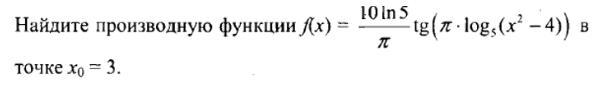
Ответы
Автор ответа:
1
Ответ: 12
Решение:
Формулы для решения:
Похожие вопросы
Предмет: Українська мова,
автор: Настя1321111
Предмет: Другие предметы,
автор: mesxidzenati
Предмет: Английский язык,
автор: ALEXANDR111111111111
Предмет: Обществознание,
автор: sasha44990
Предмет: Русский язык,
автор: kovalenkoanastasiya9