Question

СРОЧНО ПОМОГИТЕ РЕШИТЬ 10 ЗАДАЧУ ПОДРОБНО ФОТО ВНИЗУ

Answer 1

Ответ:

Острые углы треугольника равны 36° и 54°.

Объяснение:

Найти два острых угла треугольника.

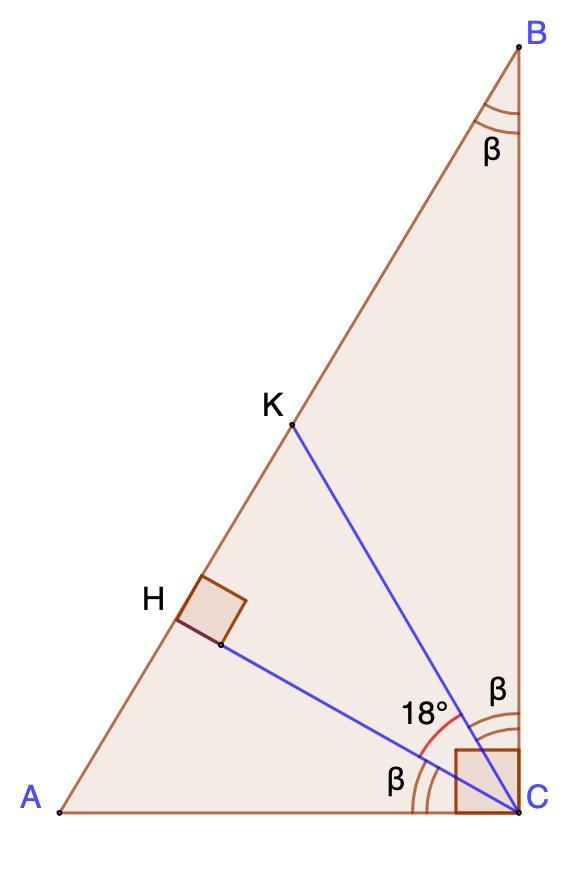
Дано: ΔАВС - прямоугольный.

∠С = 90°;

СН - высота; СК - медиана;

∠НСК = 18°.

Найти: ∠А; ∠В.

Решение:

1. Рассмотрим ΔАВС - прямоугольный.

• Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠В = 90° - ∠А

Рассмотрим ΔАНС - прямоугольный.

∠АСН = 90° - ∠А

⇒ ∠В  = ∠АСН.

Пусть ∠В  = ∠АСН = β.

2. Рассмотрим ΔСКВ.

• Медиана, проведенная из вершины прямого угла к гипотенузе, равна половине гипотенузы.

⇒ СК = КВ.

⇒ ΔСКВ - равнобедренный.

В равнобедренном треугольнике углы при основании равны.

⇒ ∠В = ∠КСВ = β

3. Рассмотрим ∠С = 90°.

∠С = ∠АСН + ∠НСК + ∠КСВ

90° = β + 18° + β

2β = 72°

β = 36°

⇒ ∠В = β = 36°

∠А = 90° - ∠В = 54°

Острые углы треугольника равны 36° и 54°.

#SPJ1