Предмет: Алгебра,
автор: lastepsey
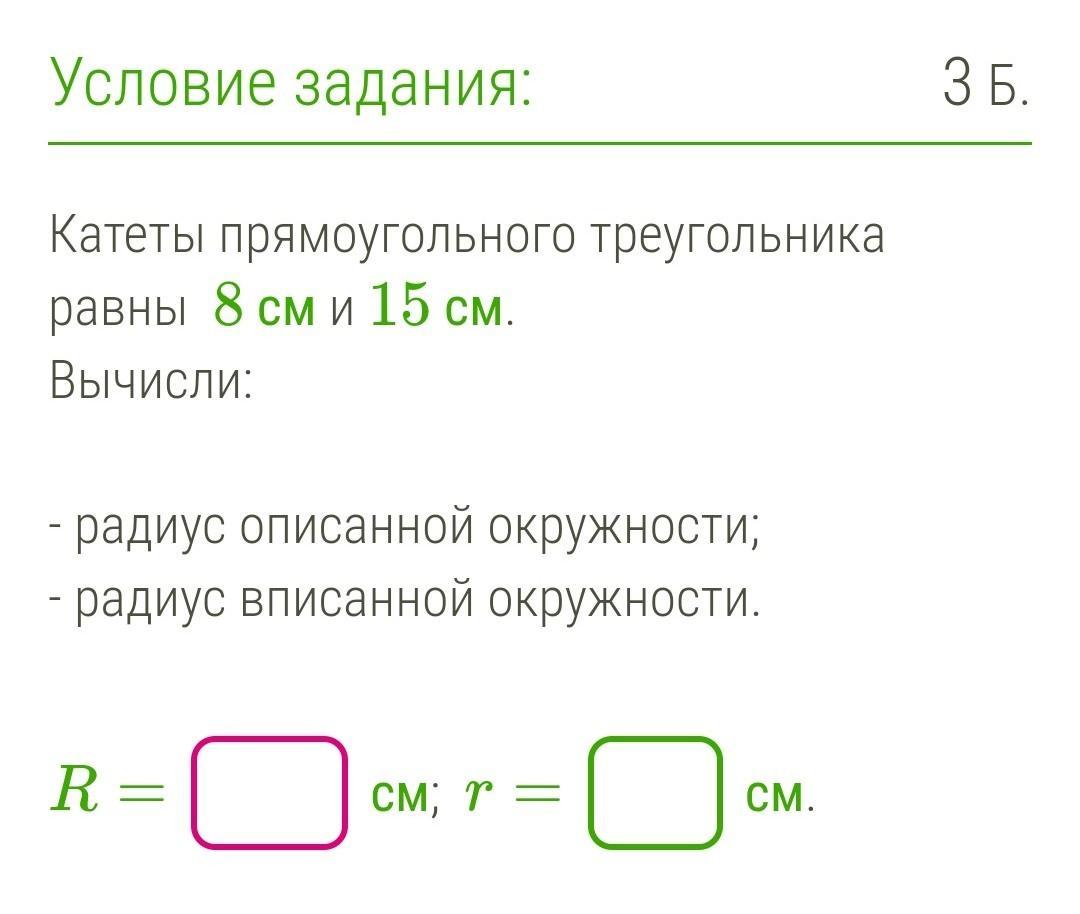
Катеты прямоугольного треугольника равны 8 см и 15 см
Приложения:
Ответы
Автор ответа:
0
Радиус описанной окружности около треугольника равен отношению сторон к 4 площади.
R = abc/4S.
S = 0,5 ab. ab - катеты.
S = 0,5*8*15=60 см^2.
По теореме Пифагора найдём гипотенузу.
с=а^2+b^2.
с=64+225=17 см.
R = 8*15*17/4*60=8,5 см.
Радиус вписанной окружности в прямоугольный треугольник равен разности полупериметра и гипотенузы.
r=p-c.
p=(8+15+17)/2 = 20 см.
r=20-17=3 см.
Ответ : R = 8,5 см ; r = 3 см.
R = abc/4S.
S = 0,5 ab. ab - катеты.
S = 0,5*8*15=60 см^2.
По теореме Пифагора найдём гипотенузу.
с=а^2+b^2.
с=64+225=17 см.
R = 8*15*17/4*60=8,5 см.
Радиус вписанной окружности в прямоугольный треугольник равен разности полупериметра и гипотенузы.
r=p-c.
p=(8+15+17)/2 = 20 см.
r=20-17=3 см.
Ответ : R = 8,5 см ; r = 3 см.
Автор ответа:
1
Ответ:
Гипотенуза прямоугольного треугольника с катетами a=8 см и b=15 см
равна см .
Радиус описанной окружности около прямоугольного треугольника
равен половине гипотенузы, то есть см .
Радиус вписанной окружности в прямоугольный треугольник
равен см .
Похожие вопросы
Предмет: Қазақ тiлi,
автор: nagibator9810
Предмет: Английский язык,
автор: ltymoshina
Предмет: Қазақ тiлi,
автор: mine6
Предмет: История,
автор: FORTNITERMalik
Предмет: Математика,
автор: dd825072