Предмет: Алгебра,
автор: Аноним
Главный мозг Помогите пожалуйста
Приложения:
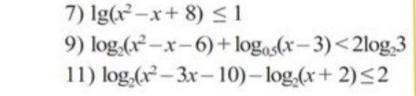
Ответы
Автор ответа:
2
Ответ:
7) [-1;2]; 9) (3;7); 11) (5;9].
Объяснение:
7) lg(x²-x+8)≤lg 10. ОДЗ: x²-x+8>0 - выполнено всюду, поскольку дискриминант отрицателен, а старший коэффициент больше нуля. Поэтому неравенство равносильно x²-x+8≤10; x²-x-2≤0; (x-2)(x+1)≤0;
x∈[-1;2].
9)
ОДЗ: На ОДЗ неравенство равносильно
x+2<9; x<7. Учитывая ОДЗ, получаем ответ: x∈(3;7).
11)
ОДЗ: На ОДЗ неравенство равносильно
x≤9. Учитывая ОДЗ, получаем ответ: x∈(5;9].
Замечание. Во всех трех задачах отбрасывание логарифмов без изменение смысла неравенств оправдывается тем, что основание логарифмов больше единицы.
Кроме того, в теме логарифмические неравенства я считаю излишним объяснять, как решаются рациональные неравенства.
Аноним:
спасибо большое
Похожие вопросы
Предмет: Английский язык,
автор: anotheropportunity
Предмет: Русский язык,
автор: vikameccc
Предмет: Русский язык,
автор: Аноним
Предмет: Химия,
автор: luba113
Предмет: Математика,
автор: Аноним