Предмет: Геометрия,
автор: okata2821
Cрочно! Знайдіть площу фігури, обмеженої заданими лініями. Виконайте
малюнок.
y=5x-3; y=x^2-5x-3
Ответы
Автор ответа:
2
Ответ:
Площадь фигуры, ограниченной линиями:
у = 5х - 3; у = х² - 5х - 3, равна (ед.²)
Объяснение:
Найти площадь фигуры, ограниченной линиями:
у = 5х - 3; у = х² - 5х - 3.
1. у = 5х - 3
- линейная функция, график прямая.
2. у = х² - 5х - 3
- парабола, ветви вниз.
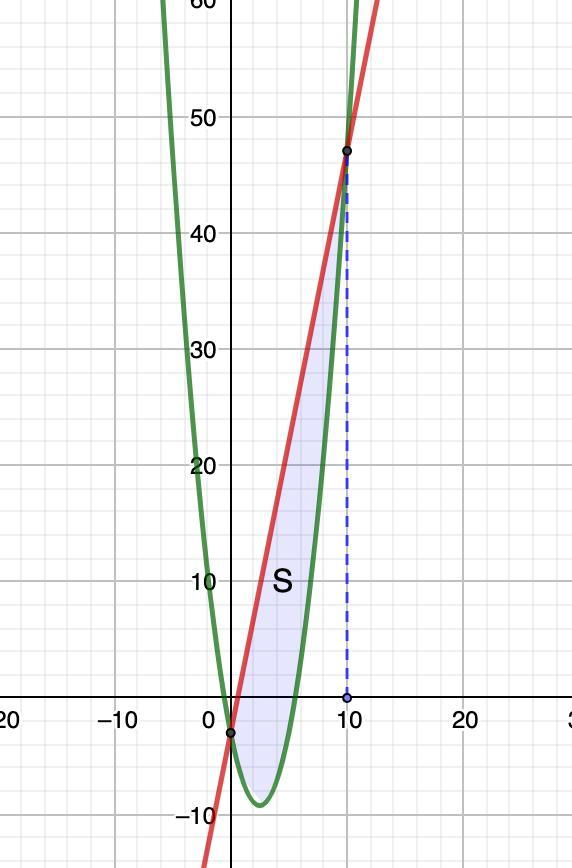
3. Найдем точки пересечения данных графиков:
х² - 5х - 3 = 5х - 3
х² - 10х = 0
х · (х - 10) = 0
х₁ = 0; х₂ = 10
4. Площадь фигуры найдем по формуле:
У нас:
b = 10 (справа); а = 0 (слева); f₂(x) = 5x - 3 (сверху); f₁(x) = x² - 5x -3 (снизу).
Найдем площадь:
Площадь фигуры, ограниченной линиями:
у = 5х - 3; у = х² - 5х - 3, равна (ед.²)
#SPJ1
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: DATERO
Предмет: Русский язык,
автор: kovalevsn62
Предмет: Русский язык,
автор: Adis11
Предмет: Математика,
автор: noname3682
Предмет: Геометрия,
автор: lekhastovpets